電流センサーのスタディ
この例では、電流センサーを対象として、従来の有限要素法と比較した積分法の利点を示します。このケースでは、
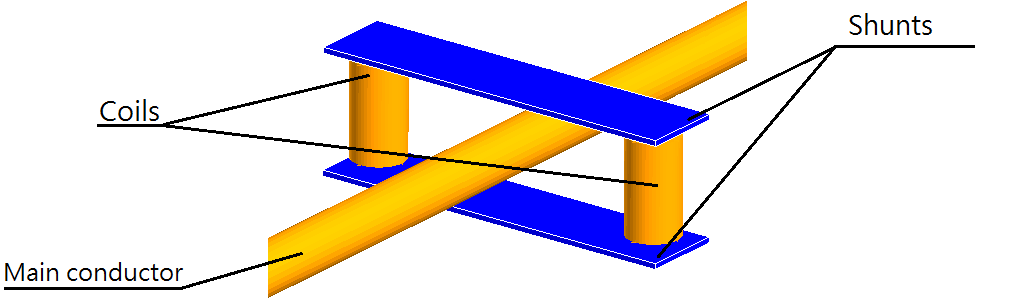
図 1 に示すように、メイン導体に電流を流し、補助コイルで観測される磁束を計算します。このセンサーの特性を記述するには、そのゲインとクロストークを知る必要があります。
図 1. デバイス全体
このデバイスの特徴は、漏洩磁束が多いこと、導体間距離が大きくなる可能性があることです。したがって、従来の有限要素法を使用するには、周囲の空気を細かくメッシュ化する必要があります。実際の解に近い結果を得るには、対称性があって高密度なメッシュにする必要があります。その結果、計算時間が長くなります(
図 2 をご参照ください)。
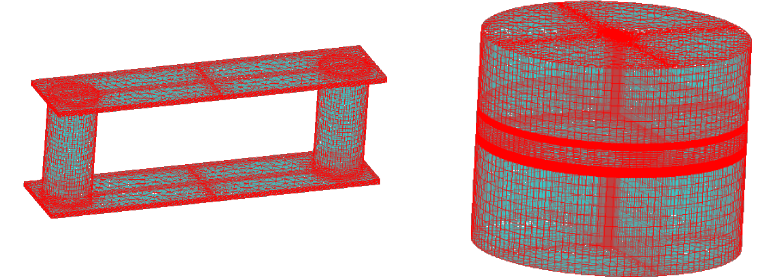
図 2. 左側はデバイスのメッシュ。右側は空気のメッシュ。
積分法では空気をメッシュ化しないので、メッシュ化要素を少なくすることができます(
図 3 をご参照ください)。
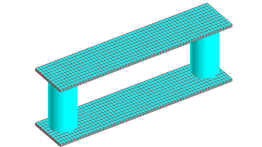
図 3. 積分法のメッシュ
2つの方法の比較:
表 1. メイン導体を流れる電流値1つの計算時間
方法
メッシュ
解析
磁束計算
積分法
2秒
30秒
1秒
有限要素法
20分
5分
20分
コイルの磁束の計算でも、体積積分法のほうが有限要素法より高速です。この磁束に影響する要因として、他方のコイルの磁束と磁性パートの磁束の2点があります。[2]空気中の磁束と他のコイルの磁束はビオ・サバール法で計算します。磁性パートの磁束は、解析で計算済みの磁気ベクトルポテンシャルを使用して計算します。
結果
このセンサーのスタディでは、目的の周波数領域で定義したセンサーのゲインが、
G
0
=
2
π
φ
f
I
0
の関係式によってわかっている必要があります。
f: 周波数
I
0
: メイン導体を流れる電流
φ
: 補助コイルの磁束
次のように、複数の電流値についてゲインを計算できます。
図 4. センサーのゲイン
図 4 を見ると、メッシュが細かいほど、結果が実際の解に近くなること、つまり積分法による解に近くなることがわかります。
すべてを求めるスタディでは、センサーのクロストーク
λ
=
G
G
0
もわかっている必要があります。
G: メイン導体の位置が占めるオフセットを考慮した、センサーのゲイン。
図 5. センサーのクロストーク
注: 積分法によるこのスタディのシミュレーションに要する合計時間:15分
注: 高密度メッシュを使用した有限要素法によるこのスタディのシミュレーションに要する合計時間:6時間
参考文献
[2]:L. Huang, G. Meunier et al., “General Integral Formulation of Magnetic Flux Computation and Its Application to Inductive Power Transfer System,” IEEE Trans. on Mag., vol. 53, no. 6, pp. 1-4, June 2017.