変換： 概要

使用の基本

変換は、作成済みのオブジェクトから新しいオブジェクトを作成できる幾何関数です。

さまざまな機能

下記のさまざまな機能を使用できます：

  • 並進
  • 回転
  • アフィニティを含む対称
  • 合成変換

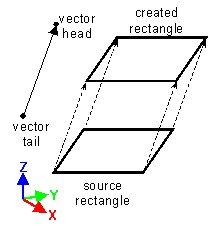
並進

並進は方向と距離によって定義されます。
並進ベクトル 2つのポイントと比率によって定義された並進
  • 方向と距離は以下によって定義されます：
    • 作業座標系
    • ベクトル（このDX、DY、およびDZ成分によってこのベクトルの方向と大きさが定義されます）
  • 方向は、2つのポイント（ベクトル後端とベクトル先端）によって定義されます。
  • 距離は、スケールファクター（比率）を使用して計算された2つのポイント（ベクトル後端とベクトル先端）間の距離に比例します。

回転

回転は回転軸と角度によって定義されます。

3つの角度と回転の中心によって定義された回転
  • 回転軸と回転角度は、以下によって定義されます：
    • 作業座標系
    • 回転の中心
    • 回転角度は、X、Y、Z軸を中心にして定義されます。

アフィニティ

アフィニティは、ポイント、直線、または平面に対して定義されます。

この変換の適用結果は、アフィニティ率に応じて異なります（下表をご参照ください）。

比率 結果
k = -1 対称
k = 1 同一
k = 0 投影
k > 1 拡大（拡大アフィニティ）
0 < k < 1 縮小（縮小アフィニティ）
k < -1 拡大（負の拡大アフィニティ）
-1 < k < 0 縮小（負の縮小アフィニティ）
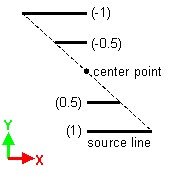
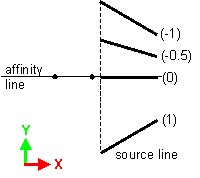
単一のポイントに対するアフィン変換 単一のラインに対するアフィン変換 単一の平面に対するアフィン変換
警告: アフィン変換のスケールファクターがk = 0の場合、ポイントに対するアフィン変換を適用するとアプリケーションでエラーが発生します。これは、関連する形状エンティティ（ポイント、ライン、フェイス、またはボリューム）は、すでに作成されているか（ポイントの場合）、すでに縮退されてポイントになっている（ライン、フェイス、またはボリュームの場合）ためです。

対称化

対称化は、k = -1である場合のアフィン変換の特殊ケースであり（上記をご参照ください）、ポイント、ライン、または平面に対して定義されます。

合成変換

2つの作成済み変換を組み合わせた合成変換を作成できます。

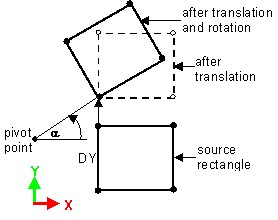
2つの変換を組み合わせた変換：

  • Y軸に沿った並進（DX=0とDYによって定義）
  • Z軸周りの回転（回転の中心と角度αによって定義）
警告: 2つの変換を異なる順序で使用した場合、同じ結果は得られません。

パラメータ設定

変換の特性は、パラメータ化された式です。ベクトル成分、回転の中心の座標、回転角度、アフィニティ率は、代数式を使用して定義できます。

この代数式には、以下を含めることができます：

  • 定数
  • 形状パラメータ（事前に作成されたもの）
  • 次の演算子を使用した基本数学関数：+、-、*、/、( )
  • FORTRANで使用できる標準数学関数

数学関数については、関数の項をご参照ください。