TO Card
Using the TO card a surface mesh in the form of a toroidal segment can be generated.
On the Construct tab, in the Surfaces group,
click the ![]() Torus (TO) icon.
Torus (TO) icon.
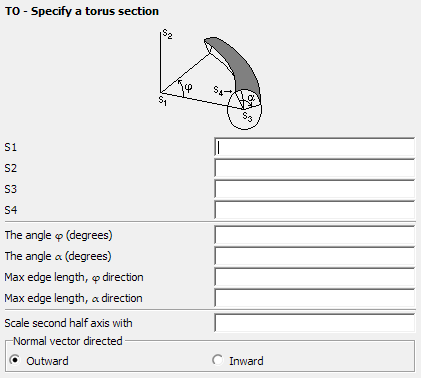
Figure 1. The Specify a torus section dialog.
Parameters:
- S1
- The centre of the toroid.
- S2
- A point that is perpendicular and is situated an arbitrary distance above the plane of the toroid.
- S3
- The start point of the axis of the toroid.
- S4
- A point on the surface of the toroidal segment. It must be in the plane S2–S1– S3.
- The angle (degrees)
- The angle of rotation around the axis S1–S2.
- The angle (degrees)
- The angle of rotation around the axis of the toroid, see the figure displayed in the card.
- Max edge length, direction
- The maximum edge length along the curved edge in the direction in m (is scaled by the SF card). If this parameter is left empty, the value specified with the IP card is used.
- Max edge length, direction
- The maximum edge length along the curved edge in the direction in m (is scaled by the SF card). If this parameter is left empty, the value specified with the IP card is used.
- Normal vector directed
- The triangles can be created so that the normal vectors point Outward (outward, away the ring axis of the toroid) or Inward.
- Scale second half axis with
- If this parameter is empty or is set to 1, a toroid with a circular cross section is created. If set to , an elliptical toroid is created by distorting the entire geometry along the second half axis (orthogonal to the axis S1–S3) with the factor where a is the distance S1–S3. It is not recommended to generate toroids where the elliptical cross section has extremely small or extremely large axial ratios with a CAD system (such as FEMAP) as the distortion formulation used in PREFEKO may fail in these cases.
A complete toroid is obtained by using the parameters and .
Examples of TO usage
The toroidal segment, which is shown in Figure 3, is generated using a TO card. This card can also be used to generate the toroidal segment with an elliptical cross section as shown in Figure 4. Note that it is stretched in the direction of the Y axis, for example, it is elliptical in the -plane. It is also elliptical in the -plane when , but it is circular in the -plane when .

Figure 2. Sketch illustrating the use of the TO card.

Figure 3. Example of an elliptical cross section created with the TO card.

Figure 4. Example of a toroidal segment with an elliptical cross section created with the TO card.