OS-T: 1090: Linear Transient Heat Transfer Analysis of an Extended Surface Heat Transfer Fin
This tutorial outlines the procedure to perform a linear transient heat transfer analysis on a steel extended-surface heat transfer fin attached to the outer surface of a system generating heat flux (Example: IC engine).
The extended surface heat transfer fin analyzed in this tutorial is one of many from an array of such fins connected to the system. The fins draw heat away from the outer surface of the system and dissipate it to the surrounding air. The process of heat transfer out of the fin depends upon the flow of air around the fin (free or forced convection). In the current tutorial, the focus is on transient heat transfer through heat flux loading and free convection dissipation.
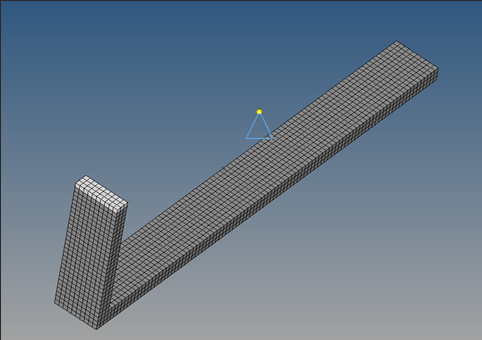
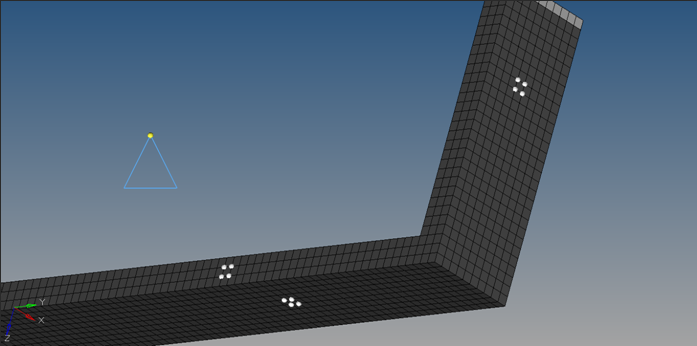
An extended surface heat transfer fin made of steel is illustrated in Figure 1. To meet certain structural design requirements, the fin is bent at 90° at approximately a quarter of its length.
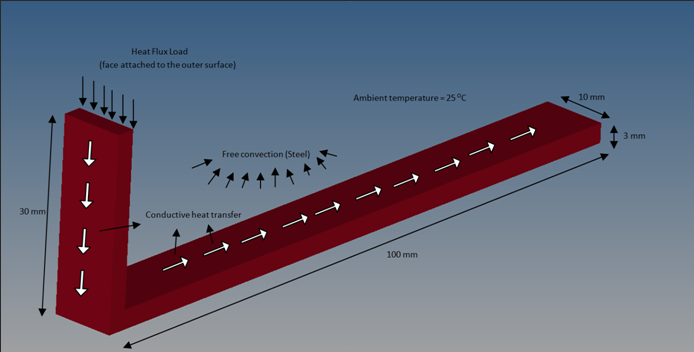
Figure 1. Extended Surface Heat Transfer Fin for Convective and Conductive Transient Heat Transfer
- The latest version of HyperMesh, HyperView and OptiStruct software installations. Transient heat transfer analysis is available only in HyperMesh version-12.0.110, HyperView version-12.0.110 and OptiStruct version-12.0.202 and later.
- The heat_transfer_fin.fem solver deck is saved on your working
directory.

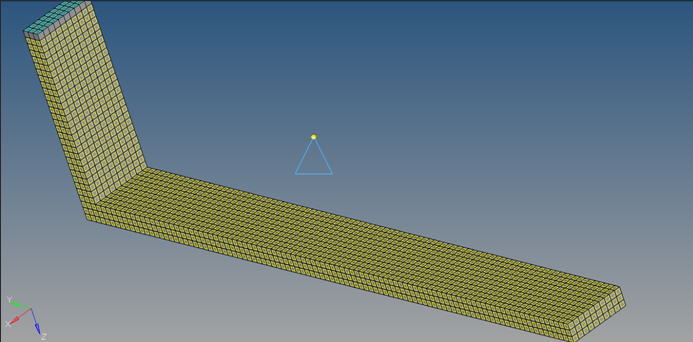
Figure 2. Heat Exchanger Fin Model for Transient Heat Transfer Analysis
Linear transient heat transfer analysis can be used to calculate the temperature distribution in a system with respect to time. The applied thermal loads can either be time-dependent or time-invariant; transient thermal analysis is used to capture the thermal behavior of a system over a specific period in time.
- Heat capacity matrix
- Conductivity matrix
- Boundary convection matrix due to free convection
- Temperature derivative with respect to time
- Unknown nodal temperature
- Thermal loading vector
The differential equation (Equation 1) is solved to find nodal temperature at the specified time steps. The difference between Equation 1 and the steady-state heat transfer equation is the term, that captures the transient nature of the analysis.
Steady-state heat transfer analysis, generally, is sufficient for a wide variety of applications. However, in situations where the system properties vary significantly over time the transient nature of heat transfer must be considered. Some examples are the relatively slow heating up of airplane gas turbine compressor disks compared to the turbine casing leading to aerodynamic issues during takeoff or the analysis of the time taken for the onset of frostbite in fingers or toes.
Launch HyperMesh and Set the OptiStruct User Profile
Import the Model
Set Up the Model
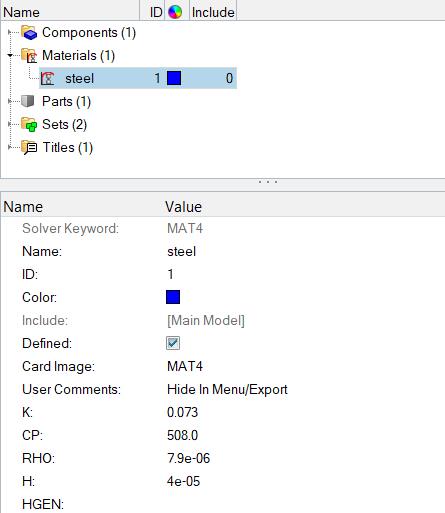
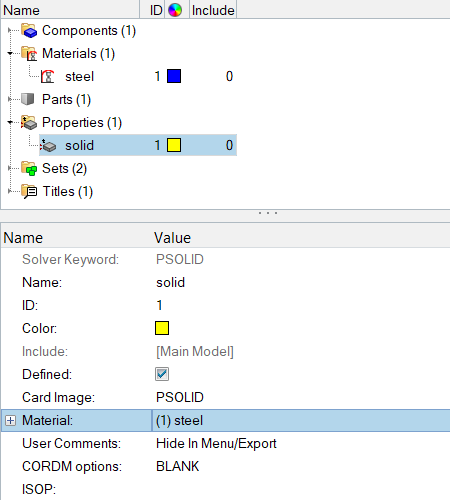
Create Thermal Material and Property
Link Thermal Material and Property to the Structure
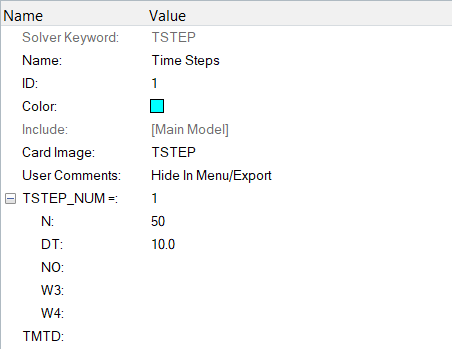
Create Transient Heat Transfer Analysis Time Steps
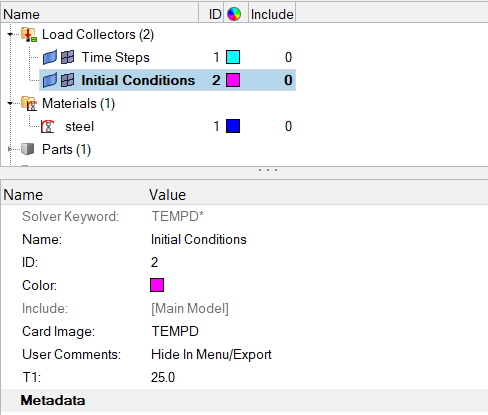
Create Transient Heat Transfer Analysis Initial Conditions
Apply Ambient Temperature Boundary Conditions
Ambient temperature thermal boundary conditions is applied on the model by creating specific load collectors for each. The ambient temperature is controlled using an SPCD entry, as this will allow an ambient temperature variation over time to help mimic such physical requirements (if any).
Create a Time-variant Ambient Temperature
Checkpoint
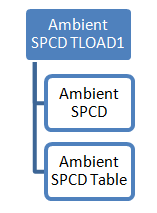
Figure 10. Process to specify a time-variant SPCD
Apply Heat Flux Load
Ambient temperature thermal boundary conditions have been assigned to the model and heat flux load from the outer surface of the engine (to which the fin is attached) is applied on the model. A time-varying heat flux load of 0 to 0.1 W/mm2 from 0 to 500 seconds is used for the analysis of this fin. This load is applied on the model by creating specific load collectors for the corresponding TLOAD1, QBDY1 and TABLED1 entries similar to the procedure used for the ambient temperature SPCD definition.
Create a Time-variant Linearly Increasing Heat Flux Load
Checkpoint
The QBDY1 flux load and its corresponding table are linked to the previously created TLOAD1 entry.
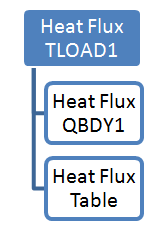
Figure 18. Process to Specify a Time-Variant SPCD
Add Free Convection
Free convection is assigned in a similar manner to the procedure used for the creation of the conduction interface. Free convection is, however, automatically assigned to all heat transfer subcases and the PCONV and CONV entries should refer to the material, steel, and the ambient temperature. The ambient temperature calculates the amount of heat transferred through free convection.
Create Surface Elements for Free Convection
Combine TLOAD1 Entries into a DLOAD Entry
Create a Transient Heat Transfer Load Step
Submit the Job
View Results
Checkpoint
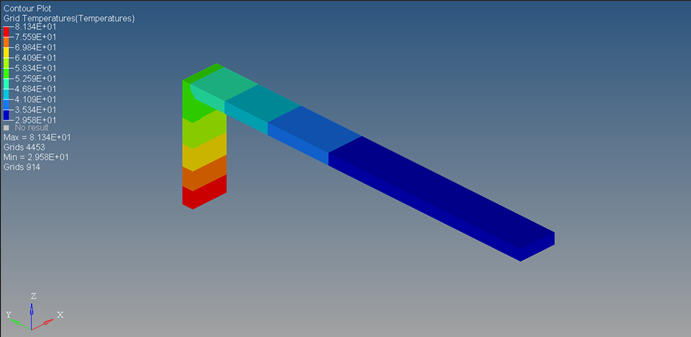
In Figure 26, this is the grid point temperature plot after 500 seconds. The system is input a linearly increasing heat flux from 0 to 0.1 W/mm2 from 0 to 500 seconds respectively. Therefore, a physical correlation can be the effect of starting an IC engine to full capacity wherein the flux transmitted to the outer surface linearly increases with time. Note that the flux patterns in actuality may be different and may fluctuate based on the duration of the power cycles. The maximum temperature of 81.3°C predictably occurs at the elements closest to the heat flux loading site and the minimum temperature of 29.5°C occurs at elements farthest from the heat source.
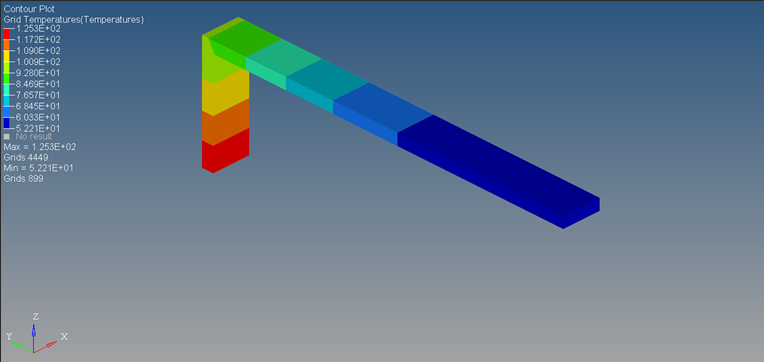
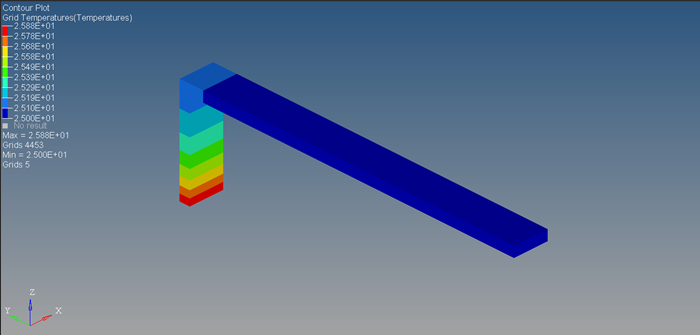
Figure 28. Grid Temperature Contour Plot after 500 Seconds - WITHOUT FREE CONVECTION
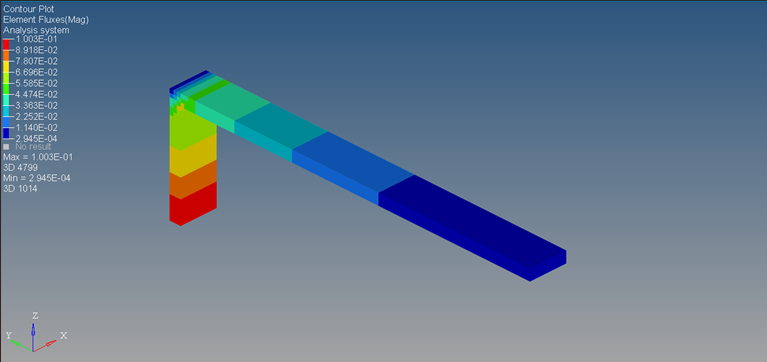
Figure 29. Contour Plot of Element Fluxes after 500 Seconds
 .
. 







 and selecting the
and selecting the  next to Data below the Dload num field.
next to Data below the Dload num field.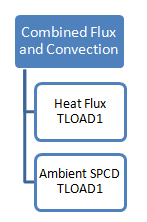
 to open the
to open the