OS-V: 0385 Simply-Supported Thick Square Plate Transient Forced Vibration Response
Test 21T OptiStruct is used to investigate the Peak Displacement in z-direction, the time at the peak displacement, extreme fiber bending stress at undamped Natural Frequency and the Static displacement at the center of the plate.
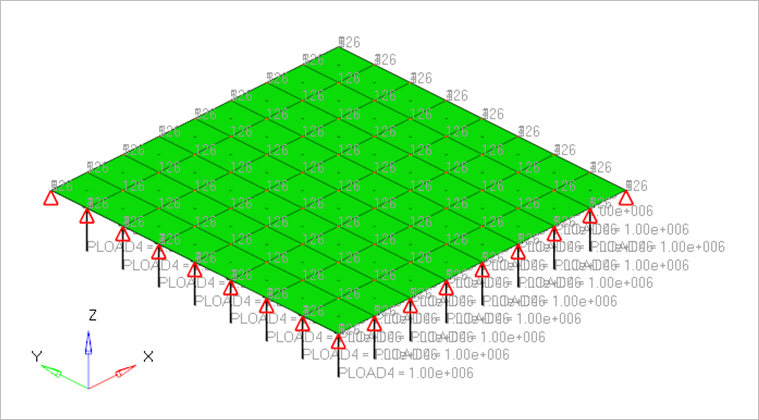
Figure 1. FE Model with Boundary Conditions and Loadcases
Benchmark Model
The 2nd order and 1st order quad elements are used to model the square plate of thickness 1.0m. The z-rotation and x, y translations are fixed for all the nodes, z-translation is fixed along all four edges, x-rotation is fixed along the edge x=0 and x=10 and y-rotation is fixed along the edge y=0 and y=10. A suddenly applied step load F0=106 N/m2 is induced in the z-direction. For modal analysis solution, a damping ratio of 0.02 is applied in all 16 modes at a time step of 0.0001 secs and for direct solution, Rayleigh damping factor α1=5.772 and α2=6.929×10-5 at a time step of 0.0001 secs are given.
- Material Properties
- Value
- Young’s Modulus
- 200 × 109 N/m2
- Poisson’s Ratio
- 0.3
- Density
- 8000 kg/m3
Frequency Response Summary
f*- Closed form solution
| Peak Displacement (mm) | Time at Peak Displacement (sec) | Peak Stress (N/mm2) | Static Displacement (mm) | |
|---|---|---|---|---|
| Reference Solution | 4.524 | 0.0108 | 62.11 | 2.333 |
| HOE: | ||||
| Direct Solution | 4.838 | 0.011 | 72.67 | 2.42 |
| Normalized | 0.935097148 | 0.981818182 | 0.854685565 | 0.964049587 |
| Modal Solution | 4.870 | 0.011 | 75.16 | 2.42 |
| Normalized | 0.928952772 | 0.981818182 | 0.82637041 | 0.964049587 |
| LOE: | ||||
| Direct Solution | 4.604 | 0.0108 | 57.98 | 2.34 |
| Normalized | 0.982623805 | 1 | 1.071231459 | 0.997008547 |
| Modal Solution | 4.611 | 0.0107 | 58.44 | 2.341 |
| Normalized | 0.981132075 | 1.009345794 | 1.062799452 | 0.996582657 |
Model Files
Refer to Access the Model Files to download the required model file(s).
- Test21THOED.fem
- Test21THOEM.fem
- Test21TLOED.fem
- Test21TLOEM.fem
Reference
NAFEMS R0016 - Selected Benchmarks for Forced Vibration, J Maguire, D J, Dawswell, L Gould 1989