OS-V: 0387 Vibrating Cylinder
Test No. CA2A numerical simulation of sound radiation of a cylinder with vibrating lateral surface radiating sound into the exterior unbounded domain.
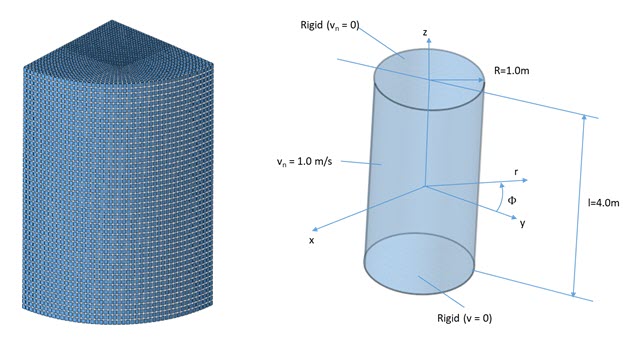
Figure 1.
OptiStruct is used to investigate the normalized sound pressure levels in the YZ plane at 100m from the origin of the coordinate system for = 0° to 90° for two wave numbers k=1 and k=2. The obtained normalized sound pressure levels are then compared with the available results of the software tools NADwork and SYSNOISE obtained from the NAFEMS Benchmark for Radiation and Scattering of Sound.
Benchmark Model
A cylinder with radius, R of 1m and length, l of 4m is modeled using QUAD4 elements with specific grid point locations. A uniform lateral surface radial velocity of v = 1.0 m/s is applied using SPCD. The end surfaces are rigid with vn = 0 using SPCs. The thickness of the plate is 0.01m.
- Property
- Value
- Young's modulus
- 200 x 109 N/m2
- Poisson's ratio
- 0.3
- Density
- 7800 kg/m3
The cylinder is enclosed within the Tetrahedral fluid elements. These fluid elements are encompassed by the CACINF3/CACINF4 Infinite elements.
- Property
- Value
- Density of the fluid (air)
- 1.225 Kg/m3
- Speed of sound
- 340 m/s
Results
Distribution of the normalized sound pressure level in the yz-plane at 100 m from the origin of the coordinate system for = 0° to 90° is listed below. The sound pressures are normalized with respect to the sound pressure at r = 100 m and = 0°.
| Phi | NADwork | SYSNOISE | OptiStruct | |||
|---|---|---|---|---|---|---|
| (K=1) | (K=2) | (K=1) | (K=2) | (K=1) | (K=2) | |
| 0 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 10 | 1.00 | 0.93 | 0.99 | 0.94 | 0.99 | 0.93 |
| 20 | 0.99 | 0.79 | 0.98 | 0.80 | 0.98 | 0.78 |
| 30 | 0.95 | 0.60 | 0.95 | 0.60 | 0.96 | 0.60 |
| 40 | 0.92 | 0.39 | 0.91 | 0.38 | 0.93 | 0.40 |
| 50 | 0.88 | 0.16 | 0.86 | 0.15 | 0.89 | 0.17 |
| 60 | 0.84 | 0.10 | 0.82 | 0.11 | 0.85 | 0.09 |
| 70 | 0.80 | 0.29 | 0.78 | 0.29 | 0.82 | 0.29 |
| 80 | 0.78 | 0.41 | 0.75 | 0.41 | 0.79 | 0.42 |
| 90 | 0.77 | 0.46 | 0.74 | 0.45 | 0.78 | 0.47 |
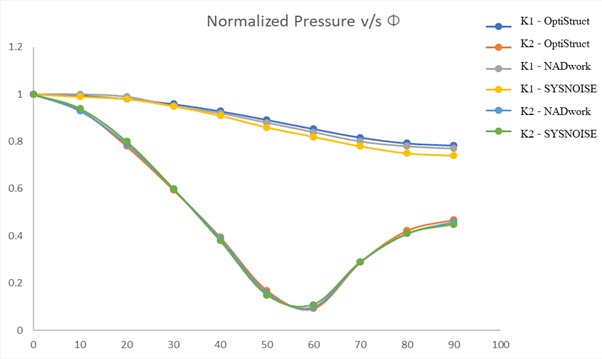
Figure 2.
Model Files
Refer to Access the Model Files to download the required model file(s).
The model files used in this problem include:
NAFEMS_CA2_IE_Cylinder.zip