fftmag
Magnitude of a Fast Fourier Transform (FFT) function. FFTMag performs a frequency analysis on a single curve's data and produces an output that indicates the magnitude of the frequency content of the input file.
Syntax
fftmag(vec_expr_1, [,vec_expr_2]|normalize)
Argument
- vec_expr_1
- The real component of a vector.
- [,vec_expr_2]|normalize
- An optional parameter that specifies the imaginary component of a
vector.
- 0 (or no input)
- The function does not divide by the number of points in vec_expr_1.
- 1
- Normalizes the output. Divides fftmag by the number of points in vec_expr_1.
Example
| Curve Math Vectors | Result |
|---|---|
x = freq(c1.x)
|
Given c1, a curve is created which is the amplitude spectrum of the FFT of c1. |
Comments
The fftmag function returns the magnitude of a Fast Fourier Transform (FFT). vec_expr_1 and vec_expr_2 are assumed to be evenly sampled. The resultant vector has a number of elements equal to the least power of two, greater than or equal to the number of elements in vec_expr_1.
If only one vector expression is passed to fftmag, the function returns a regular FFT.
If two vectors are passed to fftmag, a complex FFT is calculated. vec_expr_1 and vec_expr_2 must have the same number of elements.
The FFT is complex-valued and used to map time-domain data into the frequency domain.
The French mathematician J. Fourier (1768 - 1830) showed that any periodic motion can be represented by a series of sines and cosines. This can be demonstrated simply by considering a square wave. Such a waveform can be represented by the following Fourier series:
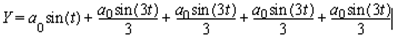
There are some very good reasons for working in the frequency domain. One of the most important is that some complicated operations in the time domain become simple in the frequency domain, for example convolution in the time domain becomes a simple multiplication in the frequency domain. In addition, the relationship between the excitation and the response of a structure is often more easily understood in the frequency domain.
Reference
Cooley, J. W., and J. W. Tukey, "An algorithm for the Machine Calculation of Complex Fourier Series", Math. Comput., 19 (April 1965): 297.