RD-E: 4400 Blow Molding with AMS

Blow molding with Advanced Mass Scaling (AMS).

The aim of this example is to introduce high quality time step control Advanced Mass Scaling (AMS). Time step will be computed by Radioss. Small element sizes may lead to small time step and; therefore, occupy many CPU sources. Increase time step could use time step control; but using old option of time step control will for example increase the mass or kinematic energy. If the increase is not small enough, it will affect the solution, but with this high-quality time step control AMS, there is no change in inertia effects on translational global acceleration, non-diagonal mass added. With AMS similar results are received, like the old one, but with much less computation time.

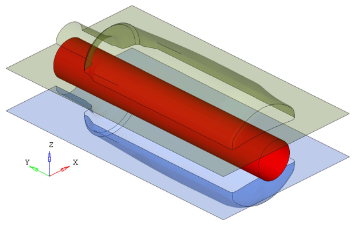
ex44_blowmold
Figure 1.

Options and Keywords Used

  • Advanced Mass Scaling (/AMS)
  • Time Step for Advanced Mass Scaling (/DT/AMS/Iflag)
  • TYPE7 interface (/INTER/TYPE7)

    TYPE7 interface has been defined between mold and plastic parison with friction 0.7.

  • Visco Elastic Plastic Piecewise Linear Material law (/MAT/LAW66)
  • Shell property (/PROP/TYPE1 (SHELL))
  • Rayleigh damping (/DAMP)
  • Rigid body (/RBODY) and Boundary condition (/BCS)

    Using rigid body, two molds have been fixed in all direction of rotation and translations of y-direction and x-direction. They are only free in z-direction (translation).

  • Impose displacement (/IMPDISP)

    Two molds are moved in opposite directions with imposed displacement.

  • Pressure Load (/PLOAD)
    The air pressure on the plastic parison is modeled using pressure load /PLOAD from inside towards outside.

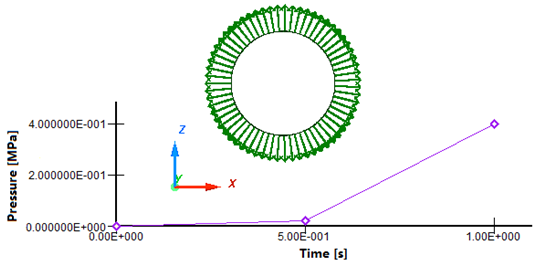
    ex44_fig2
    Figure 2. Pressure Load on Plastic Parison

Input Files

Before you begin, copy the file(s) used in this example to your working directory.

Model Description

A hollow plastic parison (tube-like) has been formed. Then the parison is clamped into a mold and air is pumped into it. Here pressure load is used to model air pressure. Let it push the plastic out and then match the mold. The dimension of the parison is cylinder with 30mm and its thickness 2mm. The dimension of the mold is 207mm x 120mm and its thickness is 1.0 mm.

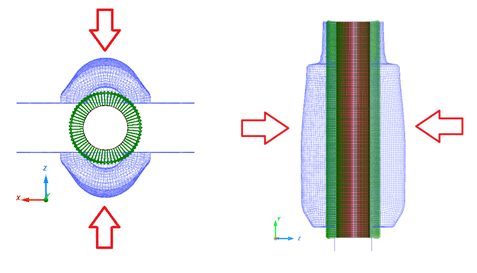
ex44_fig1
Figure 3. Problem Description for Blow Molding

Units: mm, s, Mg , N , MPa

The mold material using the Elastic model (/MAT/ELAST), with the following characteristics:
Material Properties
Initial density
7.8e-9 Mg/mm3
Young's modulus
200000 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
Poisson's ratio
0.3
The plastic parison using visco elastic plastic piecewise linear material (/MAT/LAW66), with the following characteristics:
Material Properties
Initial density
1e-9 Mg/mm3
Young's modulus
4 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@

Model Method

Blow molding using AMS will be modeled as:
  1. Define /AMS in Starter. Select the part group which will use AMS. If the part group has not been specified, then the whole model will use AMS.
  2. Use /DT/AMS in Engine. For example:
    /DT/AMS
0.67 1.15e-4

Results

The following figures show the plastic strain, von Mises stress on plastic parison.

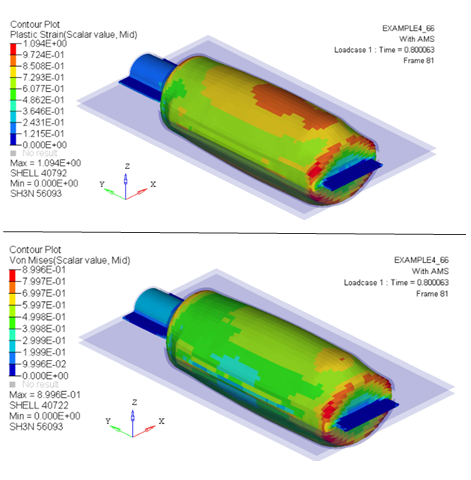
ex44_fig3
Figure 4. Plastic Strain and von Mises Stress on Plastic Parison

Performance

Using the AMS technique, CPU time is reduced by a factor of approximately 3, in this case.

Below shows results comparison of tests:
  • Without time step control (no mass scaling)
  • With standard mass scaling /DT/NODE/CST
  • With AMS
Table 1. Results of Model Computation With and Without AMS
  Without Time Step Control With Standard Mass Scaling /DT/NODA/CST With AMS
Time Step(s) 1.15e-4 0.34e-04 1.15e-4
Total Number of Cycle 78200 24280 6966
CPU Time(s) 2027.82 723.02 522.83
Speed-up - 2.80 3.88
Results Quality - Bad Good

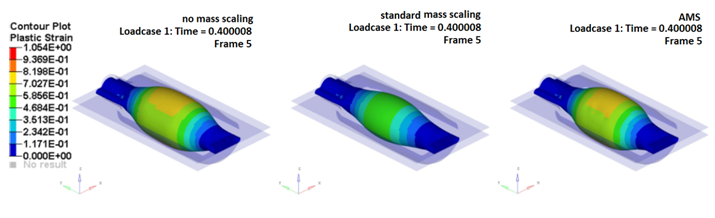
ex44_fig4
Figure 5. Plastic Strain for Tests Without Time Step Control (no mass scaling). With /DT/NODA/CST and With AMS at Time 0.4s.

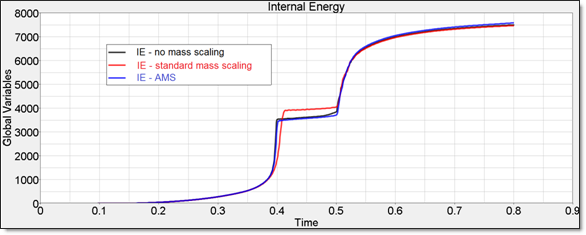
ex44_fig5
Figure 6. Internal Energy on Plastic Parison With and Without AMS

It shows at time 0.4s for the same speed up factor with AMS you get more accurate results compare with no mass scaling test than with node mass scaling.

Conclusion

To obtain a CPU saving factor of about 3, the target time step should be about 10 times higher than the one without AMS; AMS treatment itself is taking some CPU cost.

Standard mass scaling technique can also speed up the calculation by a factor of about 3, but the results quality will be affected.

In general, AMS technique for a given speed up, returns more accurate results than standard mass scaling.

The AMS technique does not change the total mass; the mass is added only on non-diagonal terms of the mass matrix.

It is applicable to the entire model.

There is no change in inertia effects on translational global acceleration.
Note:
  • Result accuracy, in terms of stress and strains, is normally not affected; by the way AMS is affecting Eigen modes of the structure(s) to which it is applied. Higher frequencies are lowered.
  • AMS technique is highly scalable; large models could show even more significant speed up factors.