The study of fatigue life of structures under random loading.
Power Spectral Density (PSD) results from the random response analysis are used to
calculate Moments
m
n
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBamaaBa
aaleaacaWGUbaabeaaaaa@3804@
The PSD Moments are calculated based on the PSD stresses generated from the random
response analysis.
Power Spectral Density (PSD) Moments
PSD Moments are calculated based on the Stress PSD generated from the random response
analysis as:
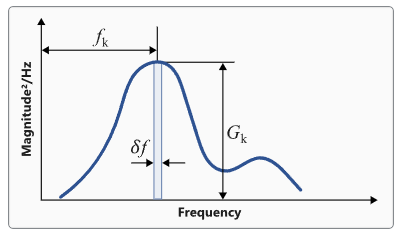
Figure 1. Calculation of PSD Moments
Moments are calculated based on:
(1)
m
n
=
∑
k
=
1
N
f
k
n
G
k
δ
f
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBamaaBa
aaleaacaWGUbaabeaakiaaykW7cqGH9aqpcaaMc8+aaabCaeaacaWG
MbWaa0baaSqaaiaadUgaaeaacaWGUbaaaOGaam4ramaaBaaaleaaca
WGRbaabeaakiabes7aKjaadAgaaSqaaiaadUgacaaMi8Uaeyypa0Ja
aGjcVlaaigdaaeaacaWGobaaniabggHiLdaaaa@4C99@
Where,
f
k
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaaDa
aaleaacaWGRbaabaaaaaaa@37FB@
Frequency value.
G
k
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4ramaaBa
aaleaacaWGRbaabeaaaaa@37DB@
PSD response value at frequency
f
k
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaaDa
aaleaacaWGRbaabaaaaaaa@37FB@
.
Calculate Probability of Stress Range Occurence
Calculation of the probability of occurrence of a stress range between the initial
and final stress range values within each bin section are user-defined.
The probability
P
Δ
S
i
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaeiuamaabm
aabaGaeyiLdqKaam4uamaaBaaaleaacaWGPbaabeaaaOGaayjkaiaa
wMcaaaaa@3BB2@
of a stress range
occuring between
Δ
S
i
− δ S / 2
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacq
GHuoarcaWGtbWaaSbaaSqaaiaadMgaaeqaaOGaaGPaVlabgkHiTiaa
ykW7cqaH0oazcaWGtbGaai4laiaaikdaaiaawIcacaGLPaaaaaa@42CE@
and
Δ
S
i
+ δ S / 2
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacq
GHuoarcaWGtbWaaSbaaSqaaiaadMgaaeqaaOGaaGPaVlabgUcaRiaa
ykW7cqaH0oazcaWGtbGaai4laiaaikdaaiaawIcacaGLPaaaaaa@42C3@
is:
(2)
P
Δ
S
i
= p δ
S
i
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
aabaGaeyiLdqKaam4uamaaBaaaleaacaWGPbaabeaaaOGaayjkaiaa
wMcaaiaaykW7cqGH9aqpcaaMc8UaamiCaiabes7aKjaadofadaWgaa
WcbaGaamyAaaqabaaaaa@445C@
Probability Density Function (Probability Density of Number of Cycles Versus
Stress Range)
PSD Moments calculated as shown above are used in the generation of a Probability
Density Function
f
m
n
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm
aabaGaamyBamaaBaaaleaacaWGUbaabeaaaOGaayjkaiaawMcaaaaa
@3A82@
DIRLIK
DIRLIK postulated a closed form solution to the determination of the
Probability Density Function as:(3)
p
S
=
D
1
Q
e
−
Z
Q
+
D
2
Z
R
2
e
−
Z
2
2
R
2
+
D
3
Z
e
−
Z
2
2
2
m
0
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaabm
aabaGaam4uaaGaayjkaiaawMcaaiaaykW7cqGH9aqpcaaMc8+aaSaa
aeaadaWcaaqaaiaadseadaWgaaWcbaGaaGymaaqabaaakeaacaWGrb
aaaiaadwgadaahaaWcbeqaamaalaaabaGaeyOeI0IaamOwaaqaaiaa
dgfaaaaaaOGaaGPaVlabgUcaRiaaykW7daWcaaqaaiaadseadaWgaa
WcbaGaaGOmaaqabaGccaWGAbaabaGaamOuamaaBaaaleaacaaIYaaa
beaaaaGccaWGLbWaaWbaaSqabeaadaWcaaqaaiabgkHiTiaadQfada
ahaaadbeqaaiaaikdaaaaaleaacaaIYaGaamOuamaaCaaameqabaGa
aGOmaaaaaaaaaOGaaGPaVlabgUcaRiaaykW7caWGebWaaSbaaSqaai
aaiodaaeqaaOGaamOwaiaadwgadaWcaaqaaiabgkHiTiaadQfadaah
aaWcbeqaaiaaikdaaaaakeaacaaIYaaaaaqaaiaaikdadaGcaaqaai
aad2gadaWgaaWcbaGaaGimaaqabaaabeaaaaaaaa@606E@
Where,
D
1
=
2
x
m
−
γ
2
1
+
γ
2
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiramaaBa
aaleaacaaIXaaabeaakiaaykW7cqGH9aqpcaaMc8+aaSaaaeaacaaI
YaWaaeWaaeaacaWG4bWaaSbaaSqaaiaad2gaaeqaaOGaaGPaVlabgk
HiTiaaykW7cqaHZoWzdaahaaWcbeqaaiaaikdaaaaakiaawIcacaGL
PaaaaeaacaaIXaGaaGPaVlabgUcaRiaaykW7cqaHZoWzdaahaaWcbe
qaaiaaikdaaaaaaaaa@4E23@
D
2
=
1
−
γ
−
D
1
+
D
1
2
1
−
R
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiramaaBa
aaleaacaaIYaaabeaakiaaykW7cqGH9aqpcaaMc8+aaSaaaeaacaaI
XaGaaGPaVlabgkHiTiaaykW7cqaHZoWzcaaMc8UaeyOeI0IaaGPaVl
aadseadaWgaaWcbaGaaGymaaqabaGccaaMc8Uaey4kaSIaaGPaVlaa
dseadaqhaaWcbaGaaGymaaqaaiaaikdaaaaakeaacaaIXaGaaGPaVl
abgkHiTiaaykW7caWGsbaaaaaa@5400@
D
3
=
1
−
D
1
−
D
2
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiramaaBa
aaleaacaaIZaaabeaakiaaykW7cqGH9aqpcaaMc8UaaGymaiaaykW7
cqGHsislcaaMc8UaamiramaaBaaaleaacaaIXaaabeaakiaaykW7cq
GHsislcaaMc8UaamiramaaBaaaleaacaaIYaaabeaaaaa@47F7@
Z
=
S
2
m
0
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOwaiaayk
W7cqGH9aqpcaaMc8+aaSaaaeaacaWGtbaabaGaaGOmamaakaaabaGa
amyBamaaBaaaleaacaaIWaaabeaaaeqaaaaaaaa@3E7A@
Q
=
1.25
γ
−
D
3
−
D
2
R
D
1
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyuaiaayk
W7cqGH9aqpcaaMc8+aaSaaaeaacaaIXaGaaiOlaiaaikdacaaI1aWa
aeWaaeaacqaHZoWzcaaMc8UaeyOeI0IaaGPaVlaadseadaWgaaWcba
GaaG4maaqabaGccaaMc8UaeyOeI0IaaGPaVlaadseadaWgaaWcbaGa
aGOmaaqabaGccaWGsbaacaGLOaGaayzkaaaabaGaamiramaaBaaale
aacaaIXaaabeaaaaaaaa@4F11@
R
=
γ
−
x
m
−
D
1
2
1
−
γ
−
D
1
+
D
1
2
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOuaiaayk
W7cqGH9aqpcaaMc8+aaSaaaeaacqaHZoWzcaaMc8UaeyOeI0IaaGPa
VlaadIhadaWgaaWcbaGaamyBaaqabaGccaaMc8UaeyOeI0IaaGPaVl
aadseadaqhaaWcbaGaaGymaaqaaiaaikdaaaaakeaacaaIXaGaaGPa
VlabgkHiTiaaykW7cqaHZoWzcaaMc8UaeyOeI0IaaGPaVlaadseada
WgaaWcbaGaaGymaaqabaGccaaMc8Uaey4kaSIaaGPaVlaadseadaqh
aaWcbaGaaGymaaqaaiaaikdaaaaaaaaa@5BC6@
x
m
=
m
1
m
0
m
2
m
4
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBa
aaleaacaWGTbaabeaakiaaykW7cqGH9aqpcaaMc8+aaSaaaeaacaWG
TbWaaSbaaSqaaiaaigdaaeqaaaGcbaGaamyBamaaBaaaleaacaaIWa
aabeaaaaGcdaGcaaqaamaalaaabaGaamyBamaaBaaaleaacaaIYaaa
beaaaOqaaiaad2gadaWgaaWcbaGaaGinaaqabaaaaaqabaaaaa@43E9@
γ
=
m
2
m
0
m
4
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4SdCMaaG
PaVlabg2da9iaaykW7daWcaaqaaiaad2gadaWgaaWcbaGaaGOmaaqa
baaakeaadaGcaaqaaiaad2gadaWgaaWcbaGaaGimaaqabaGccaWGTb
WaaSbaaSqaaiaaisdaaeqaaaqabaaaaaaa@4178@
Irregularity factor.
S
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaaaa@36CB@
Stress range.
LALANNE
The LALANNE random fatigue damage model depicts the probability density
function as:(4)
p
S
=
1
m
0
1
−
γ
2
2
π
e
−
S
2
8
m
0
1
−
γ
2
+
S
γ
4
m
0
1
+
e
r
f
S
γ
2
2
m
0
1
−
γ
2
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaabm
aabaGaam4uaaGaayjkaiaawMcaaiaaykW7cqGH9aqpcaaMc8+aaSaa
aeaacaaIXaaabaWaaOaaaeaacaWGTbWaaSbaaSqaaiaaicdaaeqaaa
qabaaaaOGaaGPaVpaalaaabaWaaOaaaeaacaaIXaGaaGPaVlabgkHi
TiaaykW7cqaHZoWzdaahaaWcbeqaaiaaikdaaaaabeaaaOqaamaaka
aabaGaaGOmaiabec8aWbWcbeaaaaGccaWGLbWaaWbaaSqabeaadaWc
aaqaaiabgkHiTiaadofadaahaaadbeqaaiaaikdaaaaaleaacaaI4a
GaamyBamaaBaaameaacaaIWaaabeaalmaabmaabaGaaGymaiaaykW7
cqGHsislcaaMc8Uaeq4SdC2aaWbaaWqabeaacaaIYaaaaaWccaGLOa
GaayzkaaaaaaaakiaaykW7cqGHRaWkcaaMc8+aaSaaaeaacaWGtbWa
aSbaaSqaaiabeo7aNbqabaaakeaacaaI0aWaaOaaaeaacaWGTbWaaS
baaSqaaiaaicdaaeqaaaqabaaaaOWaaeWaaeaacaaIXaGaaGPaVlab
gUcaRiaaykW7caWGLbGaamOCaiaadAgadaqadaqaamaalaaabaGaam
4uaiabeo7aNbqaaiaaikdadaGcaaqaaiaaikdacaWGTbWaaSbaaSqa
aiaaicdaaeqaaOWaaeWaaeaacaaIXaGaaGPaVlabgkHiTiaaykW7cq
aHZoWzdaahaaWcbeqaaiaaikdaaaaakiaawIcacaGLPaaaaSqabaaa
aaGccaGLOaGaayzkaaaacaGLOaGaayzkaaaaaa@7E24@
Where,
γ
=
m
2
m
0
m
4
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4SdCMaaG
PaVlabg2da9iaaykW7daWcaaqaaiaad2gadaWgaaWcbaGaaGOmaaqa
baaakeaadaGcaaqaaiaad2gadaWgaaWcbaGaaGimaaqabaGccaWGTb
WaaSbaaSqaaiaaisdaaeqaaaqabaaaaaaa@4178@
Irregularity factor.
S
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaaaa@36CB@
Stress range.
NARROW
The Narrow Band random fatigue damage model uses the following
probability functions:(5)
p
S
=
S
4
m
0
e
−
S
2
8
m
0
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaabm
aabaGaam4uaaGaayjkaiaawMcaaiaaykW7cqGH9aqpcaaMc8+aaeWa
aeaadaWcaaqaaiaadofaaeaacaaI0aGaamyBamaaBaaaleaacaaIWa
aabeaaaaGccaWGLbWaaWbaaSqabeaacqGHsisldaqadaqaamaalaaa
baGaam4uamaaCaaameqabaGaaGOmaaaaaSqaaiaaiIdacaWGTbWaaS
baaWqaaiaaicdaaeqaaaaaaSGaayjkaiaawMcaaaaaaOGaayjkaiaa
wMcaaaaa@4A90@
Where,
S
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaaaa@36CB@
Stress range.
By default, the number of zero crossings
n
z c r o s s
=
m
2
/
m
0
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBamaaBa
aaleaacaWG6bGaam4yaiaadkhacaWGVbGaam4CaiaadohaaeqaaOGa
aGPaVlabg2da9iaaykW7daGcaaqaamaalyaabaGaamyBamaaBaaale
aacaaIYaaabeaaaOqaaiaad2gadaWgaaWcbaGaaGimaaqabaaaaaqa
baaaaa@44DC@
n
p
e
a
k
s
=
m
4
/
m
2
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBamaaBa
aaleaacaWGWbGaamyzaiaadggacaWGRbGaam4CaaqabaGccaaMc8Ua
eyypa0JaaGPaVpaakaaabaWaaSGbaeaacaWGTbWaaSbaaSqaaiaais
daaeqaaaGcbaGaamyBamaaBaaaleaacaaIYaaabeaaaaaabeaaaaa@43CB@
for NARROW band, because the numerical
calculations involving
m
4
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBamaaBa
aaleaacaaI0aaabeaaaaa@37CF@
can sometimes lead to unstable numerical
behavior. If the signal is ideally NARROW band, the number of zero
crossings and number of peaks should be almost equal.
THREE
The Steinberg 3-band random fatigue damage model uses the following
probability function:(6)
P
S
=
0.683
a
t
2
m
0
0.271
a
t
4
m
0
0.043
a
t
6
m
0
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
aabaGaam4uaaGaayjkaiaawMcaaiaaykW7cqGH9aqpcaaMc8+aaiqa
aeaafaqabeWabaaabaGaaGimaiaac6cacaaI2aGaaGioaiaaiodaca
aMe8UaamyyaiaadshacaaMe8UaaGOmamaakaaabaGaamyBamaaBaaa
leaacaaIWaaabeaaaeqaaaGcbaGaaGimaiaac6cacaaIYaGaaG4nai
aaigdacaaMe8UaamyyaiaadshacaaMe8UaaGinamaakaaabaGaamyB
amaaBaaaleaacaaIWaaabeaaaeqaaaGcbaGaaGimaiaac6cacaaIWa
GaaGinaiaaiodacaaMe8UaamyyaiaadshacaaMe8UaaGOnamaakaaa
baGaamyBamaaBaaaleaacaaIWaaabeaaaeqaaaaaaOGaay5Eaaaaaa@6059@
Where,
S
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaaaa@36CB@
Stress range.
Unlike the other damage models, for THREE band, these values are
probability (and not probability density). This is also evident in the
use of upper case
P
S
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
aabaGaam4uaaGaayjkaiaawMcaaaaa@3929@
compared to the lower case
p
S
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaabm
aabaGaam4uaaGaayjkaiaawMcaaaaa@3949@
for the other damage models.
For the THREE damage model, these probabilities are directly used to
calculate the number of cycles by multiplying
P
S
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
aabaGaam4uaaGaayjkaiaawMcaaaaa@3929@
with the total number of zero-crossings
in the entire time history. For other damage models (except THREE), the
probability density values are first multiplied by
D
S
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiraiaado
faaaa@3794@
(bin size) to get the probability.
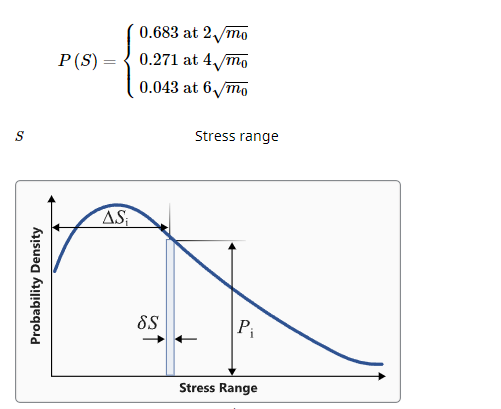
Figure 2. Probability Density Function. Probability Density of Number of Cycles Versus Stress
Range
The probability density function can be adjusted based on the following
parameters defined in the random response fatigue solution
settings.
Upper Stress Range Factor
Calculates the upper limit of the stress range as:
upper limit of the stress range = 2*RMS Stress*Upper Stress Range factor
The RMS Stress is output from random response subcase. The stress ranges of interest
are limited by the upper limit of the stress range. Any stresses beyond the upper
limit are not considered in random fatigue damage calculations.
Upper Stress Range
Directly specify the upper stress range.
Number of Bins
Calculates the width of the stress range
D
S
=
δ
S
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiraiaado
facaaMc8Uaeyypa0JaaGPaVlabes7aKjaabofaaaa@3E2B@
for which the probability is calculated (see Figure 2 ). The default is
100 and the first bin starts from 0.0 to
δ S
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiTdqMaae
4uaaaa@386E@
Stress Range Width
Directly defines the width of the stress ranges (
δ
S
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiTdqMaae
4uaaaa@386E@
).
Calculate Probability of Stress Range Occurence
Calculation of the Probability of occurrence of a stress range between the initial
and final stress range values within each bin section are based on the damage models.
DIRLIK, LALANNE, NARROW
The probability
P
S
i
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaeiuamaabm
aabaGaam4uamaaBaaaleaacaWGPbaabeaaaOGaayjkaiaawMcaaaaa
@3A4B@
of a stress range occuring between
Δ
S
i
−
δ
S
/
2
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacq
GHuoarcaWGtbWaaSbaaSqaaiaadMgaaeqaaOGaaGPaVlabgkHiTiaa
ykW7cqaH0oazcaWGtbGaai4laiaaikdaaiaawIcacaGLPaaaaaa@42CE@
and
Δ
S
i
+
δ
S
/
2
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacq
GHuoarcaWGtbWaaSbaaSqaaiaadMgaaeqaaOGaaGPaVlabgUcaRiaa
ykW7cqaH0oazcaWGtbGaai4laiaaikdaaiaawIcacaGLPaaaaaa@42C3@
is: (7)
P
S
i
=
p
i
S
i
δ S
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuamaabm
aabaGaam4uamaaBaaaleaacaWGPbaabeaaaOGaayjkaiaawMcaaiaa
ykW7cqGH9aqpcaaMc8UaamiCamaaBaaaleaacaWGPbaabeaakmaabm
aabaGaam4uamaaBaaaleaacaWGPbaabeaaaOGaayjkaiaawMcaaiab
es7aKjaadofaaaa@4684@
THREE
See Equation 6 .
For the THREE damage model, there are only three bins. The number of
cycles at each stress range (2*RMS, 4*RMS, and 6*RMS) are calculated by
directly multiplying the corresponding probabilities with the total
number of zero-crossings (refer to section below regarding calculation
of number of zero-crossings).
Select Damage Models
The following information may help assist in choosing the damage model.
The PSD moments of stress are used to calculated corresponding moments,
which are used to determine the probability density function for the
stress-range.
DIRLIK and LALANNE models generate probabilities across a wider distribution
of the stress-range spectrum. Therefore, these models should be used when
the input random signal consists of a variety of stress-ranges across
multiple frequencies. The information in the probability density function
better captures the wider range in stress-range distribution if DIRLIK and
LALANNE are used.
The NARROW model is intended for random signals for which the stress range
is expected to be closely associated with a high probability of particular
stress range distribution. Therefore, if you know the input random data does
not have a wide range of stress-range distribution, and the distribution is
mainly concentrated about a particular stress range, you should select
NARROW. This model expects the highest probability of stress-ranges to lie
at or around this particular stress range.
The THREE model is like the NARROW model, except it expects the distribution
of the random signal to contain, in addition to the association with 1*RMS,
associations (albeit smaller) with 2*RMS, and 3*RMS. Therefore, if your
input random data is mainly clustered around stress ranges in 1*RMS, and to
a lesser extent, 2*RMS, and 3*RMS, then you should select THREE.
Number of Peaks and Zero Crossings
NARROW, THREE
The number of zero crossings per second in the original time-domain
random loading (from which the frequency based random PSD load is
generated) is determined as:(8)
n
z c r o s s
=
m
2
m
0
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBamaaBa
aaleaacaWG6bGaam4yaiaadkhacaWGVbGaam4CaiaadohaaeqaaOGa
aGPaVlabg2da9iaaykW7daGcaaqaamaalaaabaGaamyBamaaBaaale
aacaaIYaaabeaaaOqaaiaad2gadaWgaaWcbaGaaGimaaqabaaaaaqa
baaaaa@44D6@
m
n
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBamaaBa
aaleaacaWGUbaabeaaaaa@3804@
Corresponding moments calculated.
DIRLIK, LALANNE
The number of peaks per second in the original time-domain random
loading (from which the frequency based random PSD load is generated) is
determined as:(9)
n
p
e
a
k
s
=
m
4
m
2
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBamaaBa
aaleaacaWGWbGaamyzaiaadggacaWGRbGaam4CaaqabaGccaaMc8Ua
eyypa0JaaGPaVpaakaaabaWaaSaaaeaacaWGTbWaaSbaaSqaaiaais
daaeqaaaGcbaGaamyBamaaBaaaleaacaaIYaaabeaaaaaabeaaaaa@43C5@
m
n
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBamaaBa
aaleaacaWGUbaabeaaaaa@3804@
Corresponding moments calculated.
Number of Cycles
NARROW band, THREE band
The total number of cycles is calculated as:(10)
N
T
=
n
z c r o s s
T
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOtamaaBa
aaleaacaWGubaabeaakiaaykW7cqGH9aqpcaaMc8UaamOBamaaBaaa
leaacaWG6bGaam4yaiaadkhacaWGVbGaam4CaiaadohaaeqaaOGaam
ivaaaa@43B5@
T
Total exposure time.
DIRLIK, LALANNE
The total number of cycles is calculated as:(11)
N
T
=
n
p e a k s
T
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOtamaaBa
aaleaacaWGubaabeaakiaaykW7cqGH9aqpcaaMc8UaamOBamaaBaaa
leaacaWGWbGaamyzaiaadggacaWGRbGaam4CaaqabaGccaWGubaaaa@42A0@
T
Total exposure time.
Total Number of Cycles of Particular Stress Range
The total number of cycles with with stress range
Δ
S
i
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyiLdqKaam
4uamaaBaaaleaacaWGPbaabeaaaaa@394C@
is calculated as:(12)
N
i
= P
Δ
S
i
N
T
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOtamaaBa
aaleaacaWGPbaabeaakiaaykW7cqGH9aqpcaaMc8Uaamiuamaabmaa
baGaeyiLdqKaam4uamaaBaaaleaacaWGPbaabeaaaOGaayjkaiaawM
caaiaad6eadaWgaaWcbaGaamivaaqabaaaaa@439F@
Fatigue Life and Damage
Fatigue life (maximum number of cycles of a particular stress range
S
i
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBa
aaleaacaWGPbaabeaaaaa@37E5@
for the material prior to failure) is calculated
based on the Material SN curve as:
(13)
N
f
S
i
=
S
i
S
f
1
b
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOtamaaBa
aaleaacaWGMbaabeaakmaabmaabaGaam4uamaaBaaaleaacaWGPbaa
beaaaOGaayjkaiaawMcaaiaaykW7cqGH9aqpcaaMc8+aaeWaaeaada
WcaaqaaiaadofadaWgaaWcbaGaamyAaaqabaaakeaacaWGtbWaaSba
aSqaaiaadAgaaeqaaaaaaOGaayjkaiaawMcaamaaCaaaleqabaWaaS
aaaeaacaaIXaaabaGaamOyaaaaaaaaaa@46F5@
Total fatigue damage as a result of the applied random loading is calculated as:
(14)
D =
∑
i = 1
N
N
i
N
f
S
i
MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiraiaayk
W7cqGH9aqpcaaMc8+aaabCaeaadaWcaaqaaiaad6eadaWgaaWcbaGa
amyAaaqabaaakeaacaWGobWaaSbaaSqaaiaadAgaaeqaaOWaaeWaae
aacaWGtbWaaSbaaSqaaiaadMgaaeqaaaGccaGLOaGaayzkaaaaaaWc
baGaamyAaiaaykW7cqGH9aqpcaaMc8UaaGymaaqaaiaad6eaa0Gaey
yeIuoaaaa@4B32@
To account for the mean stress correction with any loading that leads to a mean
stress different from zero, you can define a static subcase that consists of such
loading (typically gravity loads). This static subcase can be referenced in random
fatigue analysis event setup.