Spot Weld Fatigue Analysis

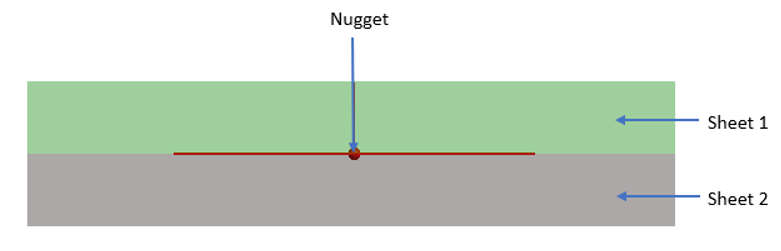
Allows for the study of fatigue performance of spot welds in structures.

Currently, only stress-life (SN) based spot weld fatigue analysis is supported. The spot weld location is defined by three attributes, sheet 1, sheet 2, and the nugget.

Implementation

Fatigue analysis for spot welds involves examining the weld at three distinct locations, the sheets and nugget, and is based on a paper by Rupp et al. The cross-sectional forces and moments at the nugget location are determined and used to calculate corresponding stresses at the sheets and the nugget. These stresses are then used to calculate Fatigue Damage using Rainflow counting and the SN approach.

The following sections illustrate how stresses and subsequently damage are calculated at each of the three locations.

Sheet Location (1 or 2)

Radial stresses are calculated at the sheet by considering forces and moments at the nugget. The radial stresses

σ (θ)

$σ (θ)$ are calculated as a function of

θ

$θ$ for each point in the load-time history as:(1)

σ (θ) = - σ_{\max} (f_{y}) \cos θ - σ_{\max} (f_{z}) \sin θ + σ (f_{x}) + σ_{\max} (m_{y}) \sin θ - σ_{\max} (m_{z}) \cos θ

$σ (θ) = - σ_{\max} (f_{y}) \cos θ - σ_{\max} (f_{z}) \sin θ + σ (f_{x}) + σ_{\max} (m_{y}) \sin θ - σ_{\max} (m_{z}) \cos θ$

Where,(2)

σ_{\max} (f_{y}) = \frac{f_{y}}{π D T} \times C_{f y z} \times D^{d e f y z} \times T^{t e f y z}

$σ_{\max} (f_{y}) = \frac{f_{y}}{π D T} \times C_{f y z} \times D^{d e f y z} \times T^{t e f y z}$

(3)

σ_{\max} (f_{z}) = \frac{f_{z}}{π D T} \times C_{f y z} \times D^{d e f y z} \times T^{t e f y z}

$σ_{\max} (f_{z}) = \frac{f_{z}}{π D T} \times C_{f y z} \times D^{d e f y z} \times T^{t e f y z}$

(4)

σ (f_{x}) = (\frac{1.744 f_{x}}{T^{2}}) \times C_{f x} \times D^{d e f x} \times T^{t e f x} for f_{x} > 0.0

$σ (f_{x}) = (\frac{1.744 f_{x}}{T^{2}}) \times C_{f x} \times D^{d e f x} \times T^{t e f x} for f_{x} > 0.0$

(5)

(f_{x}) = 0.0 for f_{x} \geq 0.0

$(f_{x}) = 0.0 for f_{x} \geq 0.0$

(6)

σ_{\max} (m_{y}) = (\frac{1.872 m_{y}}{D T^{2}}) \times C_{m y z} \times D^{d e m y z} \times T^{t e m y z}

$σ_{\max} (m_{y}) = (\frac{1.872 m_{y}}{D T^{2}}) \times C_{m y z} \times D^{d e m y z} \times T^{t e m y z}$

(7)

σ_{\max} (m_{z}) = (\frac{1.872 m_{z}}{D T^{2}}) \times C_{m y z} \times D^{d e m y z} \times T^{t e m y z}

$σ_{\max} (m_{z}) = (\frac{1.872 m_{z}}{D T^{2}}) \times C_{m y z} \times D^{d e m y z} \times T^{t e m y z}$

$D$ $D$: Diameter of the weld element
$T$ $T$: Thickness of the sheet under consideration for damage calculation
$C_{f y z}$ $C_{f y z}$ , $C_{m y z}$ $C_{m y z}$ , $C_{f x}$ $C_{f x}$: Scale factors
$d e f y z$ $d e f y z$ , $d e m y z$ $d e m y z$ , $d e f x$ $d e f x$: Diameter exponents
$t e f y z$ $t e f y z$ , $t e m y z$ $t e m y z$ , $t e f x$ $t e f x$: Thickness exponents

To be equivalent to the Rupp method:

C_{f y z} = 1, d e f y z = 0, t e f y z = 0

$C_{f y z} = 1, d e f y z = 0, t e f y z = 0$

C_{m y z} = 0.6, d e m y z = 0, t e m y z = 0.5

$C_{m y z} = 0.6, d e m y z = 0, t e m y z = 0.5$

C_{f x} = 0.6, d e f x = 0, t e f x = 0.5

$C_{f x} = 0.6, d e f x = 0, t e f x = 0.5$

The equivalent radial stresses are calculated at intervals of $θ$ $θ$ (Default =18 degrees). The value of $θ$ $θ$ can be modified by varying the Number of angles field in the spot weld solution settings. Subsequently, Rainflow cycle counting is used to calculate fatigue life and damage at each angle ( $θ$ $θ$ ). The worst damage value is then picked for output. A similar approach is conducted for the other sheet.

Nugget Location

The absolute maximum principal stresses are calculated using the shear stress and bending stress of the beam element as a function of

θ

$θ$ for each point in the load-time history as:(8)

τ (θ) = τ_{\max} (f_{y}) \sin θ + τ_{\max} (f_{z}) \cos θ

$τ (θ) = τ_{\max} (f_{y}) \sin θ + τ_{\max} (f_{z}) \cos θ$

(9)

σ (θ) = σ (f_{x}) + σ_{\max} (m_{y}) \sin θ - σ_{\max} (m_{z}) \cos θ

$σ (θ) = σ (f_{x}) + σ_{\max} (m_{y}) \sin θ - σ_{\max} (m_{z}) \cos θ$

Where,(10)

τ_{\max} (f_{y}) = \frac{16 f_{y}}{3 π D^{2}}

$τ_{\max} (f_{y}) = \frac{16 f_{y}}{3 π D^{2}}$

(11)

τ_{\max} (f_{z}) = \frac{16 f_{z}}{3 π D^{2}}

$τ_{\max} (f_{z}) = \frac{16 f_{z}}{3 π D^{2}}$

(12)

σ (f_{x}) = \frac{4 f_{x}}{π D^{2}} for f_{x} > 0.0

$σ (f_{x}) = \frac{4 f_{x}}{π D^{2}} for f_{x} > 0.0$

(13)

σ (f_{x}) = 0.0 for f_{x} \leq 0.0

$σ (f_{x}) = 0.0 for f_{x} \leq 0.0$

(14)

σ_{\max} (m_{y}) = \frac{32 m_{y}}{π D^{3}}

$σ_{\max} (m_{y}) = \frac{32 m_{y}}{π D^{3}}$

(15)

σ_{\max} (m_{z}) = \frac{32 m_{z}}{π D^{3}}

$σ_{\max} (m_{z}) = \frac{32 m_{z}}{π D^{3}}$

$D$ $D$: Diameter of the weld element
$T$ $T$: Thickness of the sheet under consideration for damage calculation

The equivalent maximum absolute principal stresses are calculated for each $θ$ $θ$ from $τ (θ)$ $τ (θ)$ and $σ (θ)$ $σ (θ)$ . These stresses are used for subsequent fatigue analysis. Rainflow cycle counting is used to calculate fatigue life and damage at each angle ( $θ$ $θ$ ). The worst damage value is then picked for output.