HS-2000: DOE Method Comparison: Arm Model Study
Learn how to set up DOEs using different methods and then compare methods for accuracy and efficiency.
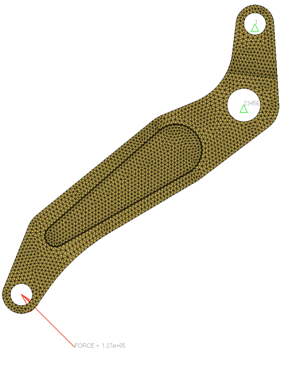
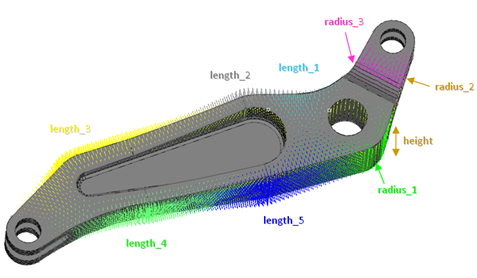
- Shape input variables
- Length1: Lower Bound = -0.5, Initial Bound = 0.0, Upper Bound = 2.0
- Output responses
- Volume (Nominal design volume 1.7667e6 mm3)
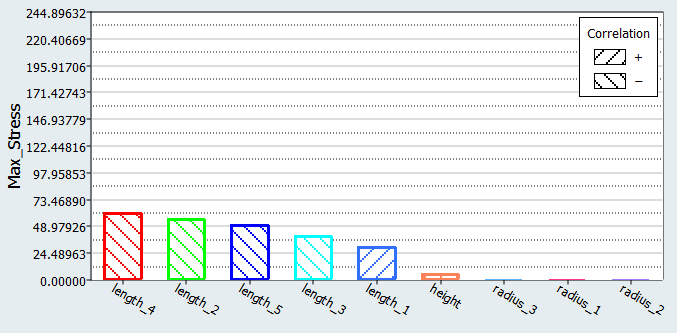
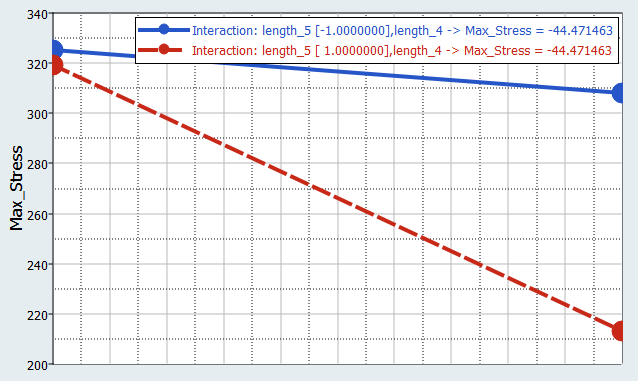
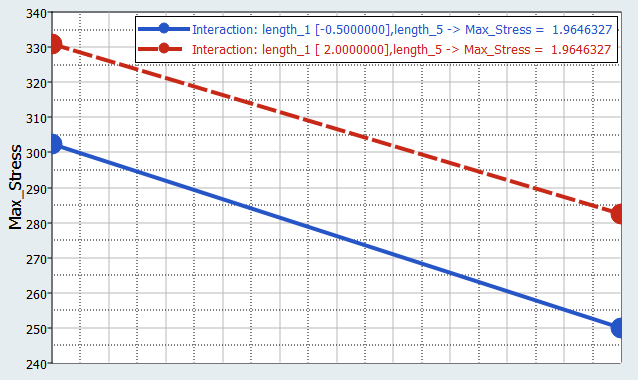
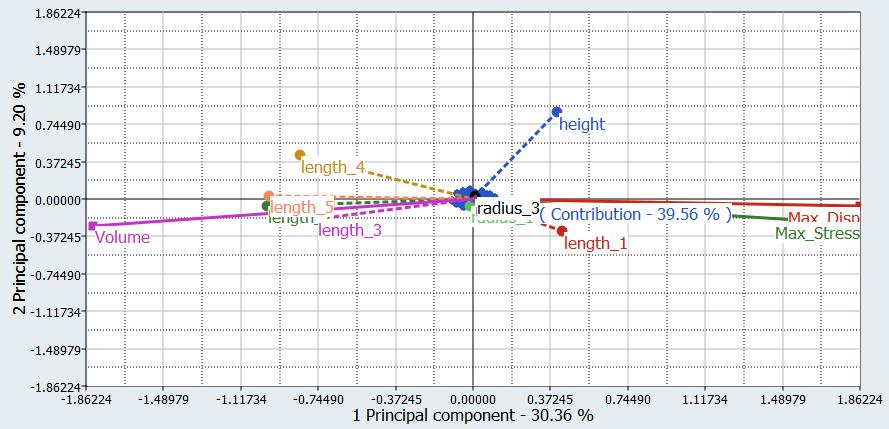
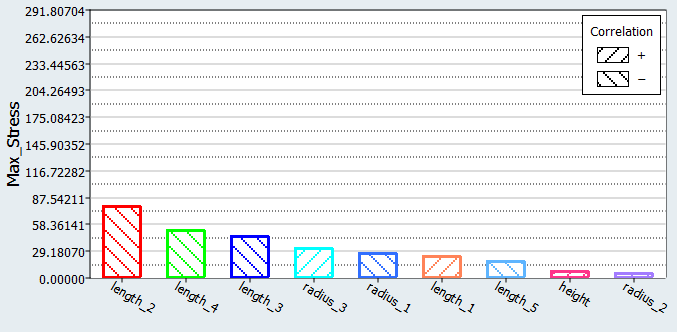
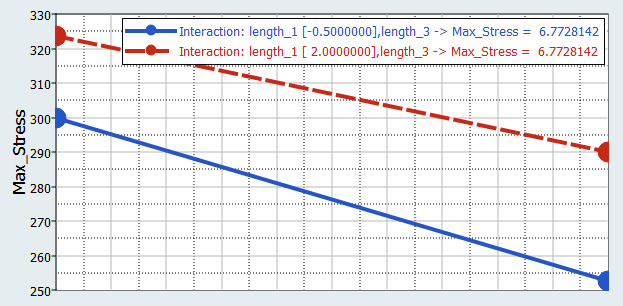
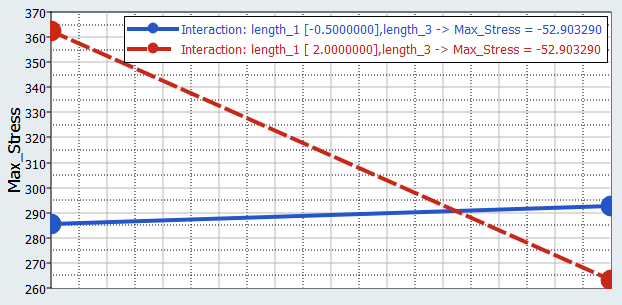
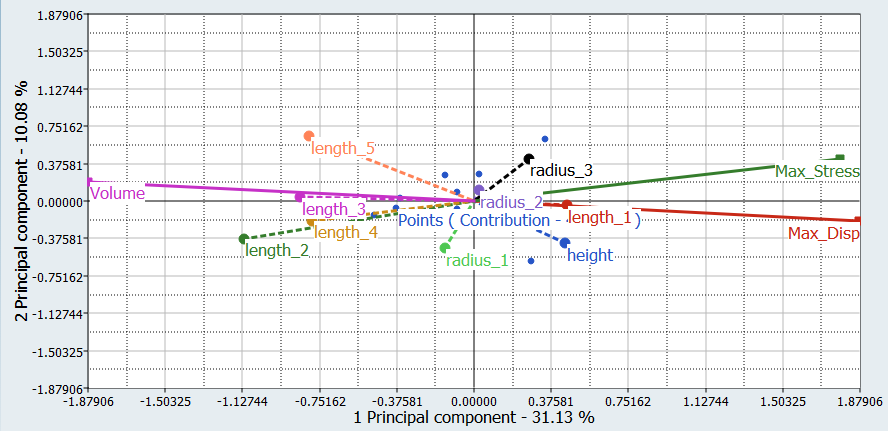
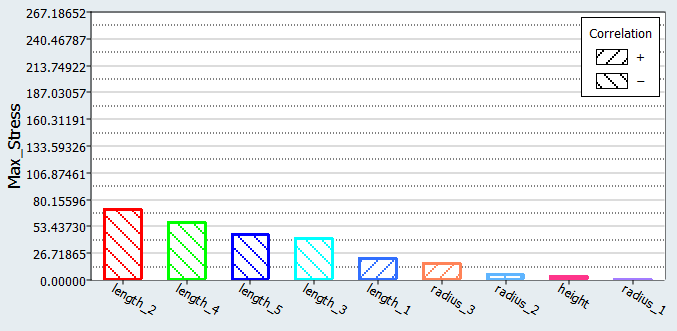
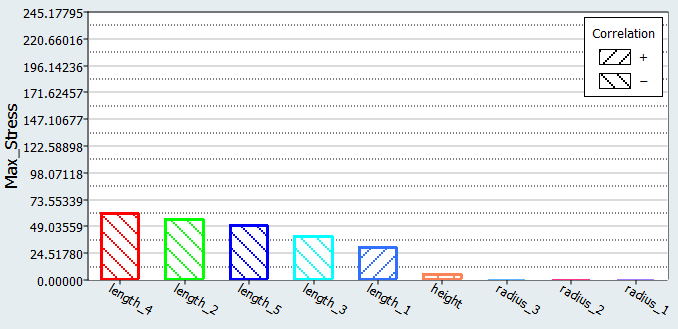
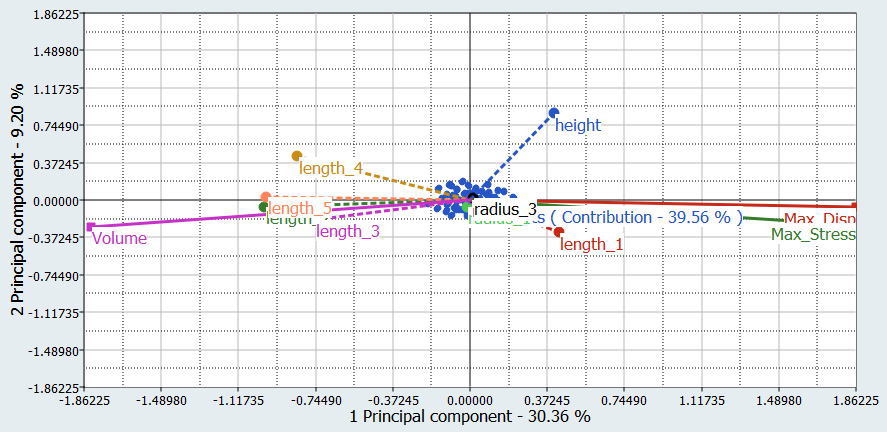
You will study the results from different parameter screening DOEs. For each screening, only the results obtained on the Max_stress output response will be reviewed using Pareto plot, Interactions, and Ordination displays.
- A Full Factorial provides excellent resolution but typically requires an exceedingly large number or runs.
- A Fractional Factorial with a Resolution III confounds main effects with interactions; results could be inaccurate if interactions are significant.
- A Fractional Factorial with a Resolution IV main effects are not confounded, but interactions are confounded with each other.
- A Fractional Factorial with a Resolution V main effects and interactions are not confounded.
Perform the Study Setup
In this step you will start from an already morphed model. The shape variables are already exported for HyperStudy and a template is created.
Perform Nominal Run
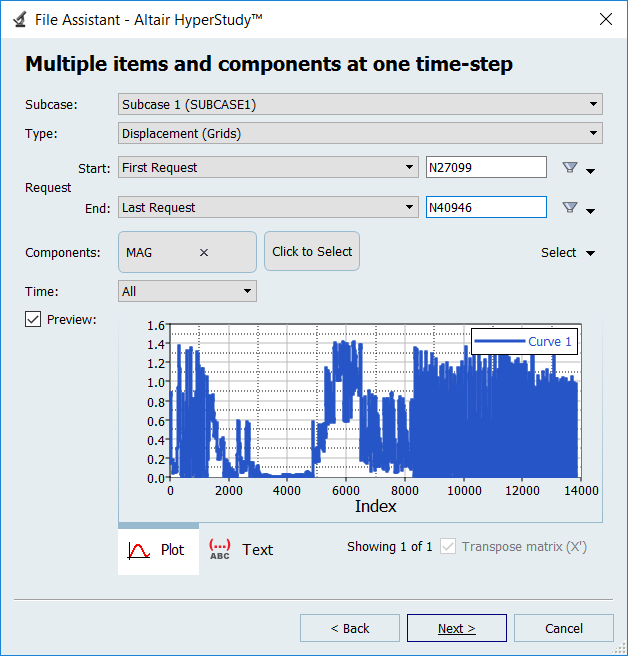
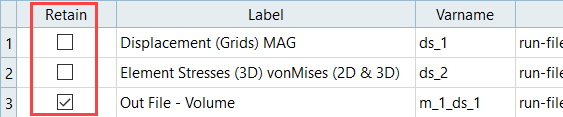
Create and Evaluate Output Responses
In this step you will create three output responses: Max_Disp, Max_Stress, and Volume.
Run Full Factorial DOE
In this step you will create a Full Factorial DOE, and set the shape variables to two levels.
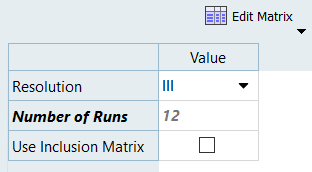
Run Fractional Factorial DOE with Resolution III
In this step you will set up a Fractional Factorial DOE, with resolution III and the same levels as the previous Full Factorial DOE.
Use the nine input variables with two levels, without turning on any interaction, leads to a 12 run Fractional Factorial plan.
Run Fractional Factorial DOE with Resolution IV
In this step you will set up a Fractional Factorial DOE with Resolution IV. Using the nine input variables with two levels, without turning on any interaction, leads to a 24 run Fractional Factorial plan.
Run Fractional Factorial DOE with Resolution V
In this step you will set up a Fractional Factorial DOE with Resolution V. Using the nine input variables with two levels, without turning on any interaction, leads to a 128 run Fractional Factorial plan.
Comparison
Conclusions on the screened output responses are summarized for the four DOE methods.
In this tutorial, you focused on the Max_Stress output response, but the same steps should be applied for all output responses.
| Full Factorial | Fractional Factorial V | Fractional Factorial IV | Fractional Factorial III | |
|---|---|---|---|---|
| Number of runs | 512 | 128 | 24 | 12 |
| Max_Stress | Remove all radii and height | Remove all radii and height | Remove radii 1, 2 and height | Remove radius 2 and height |
| Max_Disp | Remove all radii | Remove all radii | Remove all radii | Remove all radii |
| Volume | Remove all radii | Remove all radii | Remove all radii | Remove all radii |
| Conclusion | Remove all radii | Remove all radii | Remove radii 1 and 2 | Remove radius 2 |
 .
.