運動特性
概要
磁気機械連成の場合、動力学方程式を解くために、移動パートおよび連成荷重の運動特性を定義する必要があります。
Fluxでの処理
下の図は、Fluxでの運動の処理を示しています。
- 固定パート、移動パート、および圧縮性領域は、有限要素ドメインに属しています。
- 移動パートは機械的に外部デバイスに結合され、この外部デバイスには有限要素ドメイン外の荷重が連成されます。
機械的特性と運動特性
基本的な動力学方程式を解くために必要な機械的特性と運動特性は次のとおりです：
- 移動パートおよび連成荷重の質量または慣性モーメント
- 移動パートおよび連成荷重に作用する抵抗力またはトルク
- 初期条件： 移動パートの初期位置と初速度
抵抗力またはトルク
抵抗力またはトルクは、以下のような方法で記述できます：
- 事前定義済みの式： 摩擦力、復帰力（ばね）
- 可変式、ユーザーによる入力
この2つのタイプの式については、以降のブロックで詳しく説明します。
事前定義済みの式（1）
力または抵抗トルクは、摩擦力またはトルクタイプの事前定義済みの式により記述できます。
| （1）摩擦力またはトルク | |
|---|---|
| 並進 | 回転 |
 |
 |
 |
 |
方程式の符号は次のように定義されます：
- 速度が正の場合（
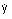または
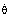> 0）：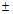 
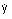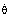の符号は+符号に置換されます。 - 速度が負の場合（または > 0）：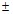
の符号は-符号に置換されます。
3つの係数f0、f1、およびf2は、次のようになります：
-
f0： 一定の摩擦係数、速度に無関係（NまたはN.m）
-
f1： 粘性摩擦係数、速度の関数（N.s/mまたはN.m.s/度）
-
f2： 摩擦係数、速度の2乗の関数（N.s2/m2またはN.m.s2/度2）
注: 対称性と周期性がある場合：
係数f0、f1、およびf2は、デバイスが全体的に表されていなくても、デバイス全体に対して定義する必要があります。力またはトルクはデバイス全体に対して計算されます。
事前定義済みの式（2）
力または抵抗トルクは、復帰力またはトルクタイプの事前定義済みの式により記述できます。
| （2）復帰力またはトルク（ばね） | |
|---|---|
| 並進 | 回転 |
 |
 |
係数kは、ばねの剛性（またはねじれ）定数です
（N/mまたはN.m/度）。
I/Oパラメータを使用した式
力または抵抗トルクは、I/Oパラメータを使用した式を介して記述できます。
I/Oパラメータを使用した式は、考慮されるメカニカルセットの位置、速度および加速度、別のメカニカルセットの関数、任意のパラメータの関数など、運動パラメータの式関数です。