磁気システムのマクスウェルの方程式
概要
マクスウェルの方程式は、電磁気学の基本法則です。
この方程式は、領域の電荷密度qと電流密度
を、その電荷と電流によって発生する電磁界に次のように関連付けます：
- 電界強度
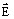と電束密度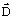
- 磁束密度
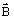と磁界強度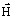
一般形
マクスウェルの方程式の一般形は次のとおりです：
マクスウェル-ガウスの式：
（1）
マクスウェル-ファラデーの式：
（2）
磁気に関するガウスの法則：
（3）
マクスウェル-アンペールの式：
（4）
その他の方程式
上記の方程式に次の材料の構成則が追加されます：
導電媒質の特性：
（5）
磁性媒質の特性：
（6）
誘電媒質の特性：
（7）
ここで：
- σ： 材料の導電率（S）
- μ： 透磁率（H/m）
- ε： 誘電率（F/m）
分離
低周波では、電界の
と
の方程式と、磁界の
と
の方程式を切り離すことができます。
したがって、次のように電気システムのマクスウェルの方程式と磁気システムのマクスウェルの方程式が存在します：
- 電界に使用する方程式群
- 磁界に使用する別の方程式群
この分離は、材料、周波数、およびスタディドメインの寸法に依存します。通常、ACアプリケーションでのマクスウェル方程式の分離は、f < 1～10GHzの周波数範囲で動作する技術デバイスに適用できます。
磁気システム向けマクスウェル方程式の形式
磁気システムの場合は、準定常状態の前提を使用し、電束密度Dの時間変化を無視します（変位電流を無視します）。準定常状態の前提は、周波数が一定の限度を超えない限り有効です。これにより、方程式4の
項の値は0になります。
したがって、この方程式は次のように書き換えることができます：
マクスウェル-ファラデーの式：
（2）
磁気に関するガウスの法則：
（3）
マクスウェル-アンペールの式：
（4）
導電媒質の特性：
（5）
磁性媒質の特性：
（6）