RD-V: 0510 Prandtl-Meyer Expansion Fan
An expansion wave appears in a supersonic flow as it turns around a convex corner.
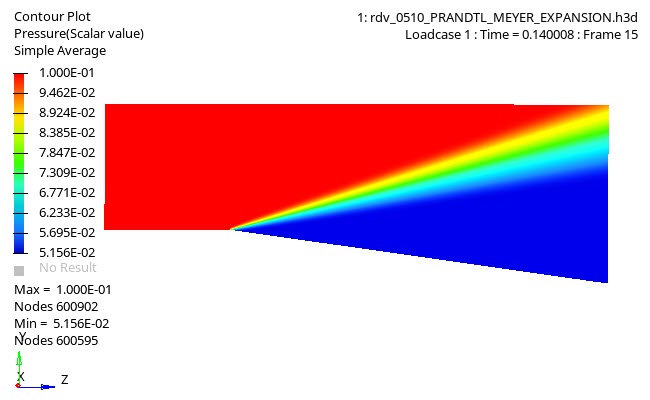
図 1.
The Prandtl-Meyer expansion fan is a classic example of incompressible fluid mechanics. It involves a supersonic flow propagating along with a convex corner. As the flow turns around the corner, it gradually loses pressure and accelerates. This process is considered isentropic and happens through an infinity of small steps forming a visible fan. The numerical results obtained for the thermodynamics variables in each state can be compared to analytical values obtained using compressible fluid mechanics theory.
Options and Keywords Used
- Fluid material, /MAT/LAW6 (HYDROまたはHYD_VISC)
- Multi-fluid law using the FVM solver, /MAT/LAW151 (MULTIFLUID)
- Ideal gas EOS, /EOS/IDEAL-GAS または /EOS/IDEAL-GAS-VE
- Second order integration scheme, /ALE/MUSCL
- Inlet boundary condition, /EBCS/INLET
- Outlet boundary condition, /EBCS/FLUXOUT
- Initial fluid velocity, /INIVEL/FVM
Input Files
必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。
Model Description
A supersonic wind tunnel (80 mm length, 20 mm height) is filled with a supersonic flow (M=3) of air.
The lower wall includes a convex corner with a downward angle of 8 degrees.
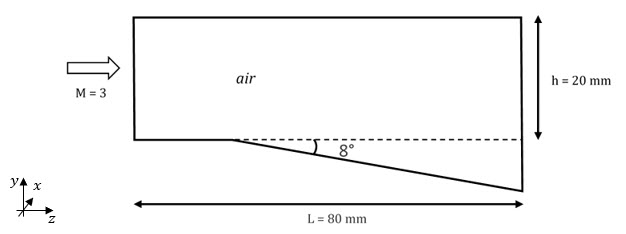
図 2. Problem Description for the Prandtl-Meyer Expansion Fan
Units: mm, ms, g, N, MPa
Model Method
The fluid domain is meshed with quads elements with an average mesh size of 0.12*0.12 mm. This accounts for around 130 000 elements.
The material law used for air is a hydrodynamic fluid (/MAT/LAW6) in combination with an ideal gas equation of state (/EOS/IDEAL-GAS).
The hydrodynamic fluid (/MAT/LAW6) is used within a multifluid law (/MAT/MULTILFUID) which uses a Finite Volume solver. The fluid is considered non-viscous.
- /MAT/LAW6
- Initial density
- /EOS/IDEAL-GAS
- Heat capacity ratio
- 1.4
- Initial pressure
- 0.1 MPa
- Initial density
Since there is only one fluid (air), the multi-material law only integrates the air defined using LAW6, with a volume fraction of 1.
To indicate that it is an EULERIAN material, /EULER/MAT should be defined for the /MAT/MULTIFLUID material.
The /ALE/MUSCL option activates a full second-order integration scheme in time and space. It should be added for more precision.
Boundary Conditions
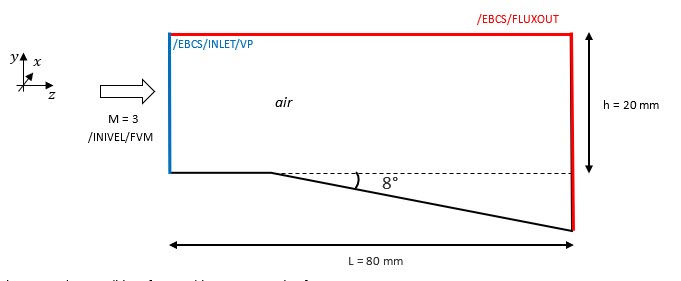
図 3. Boundary Conditions for Prandtl-Meyer Expansion Fan
When using /MAT/MULTIFLUID, the default boundary conditions are sliding walls.
A non-reflecting boundary is defined using /EBCS/INLET/VP. Input density and pressure are defined for the air in the multi-material law.
A non-reflecting boundary is defined with /EBCS/FLUXOUT.
Engine Control
As of the Radioss 2019.0 release, the critical time step scale factor for all ALE and EULER elements default to 0.5.
/DT/ALE
0.5 0.000000Results
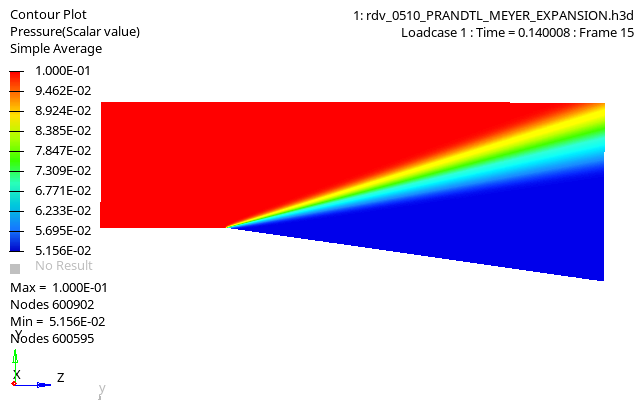
図 4. Pressure Contour of Fluid Domain
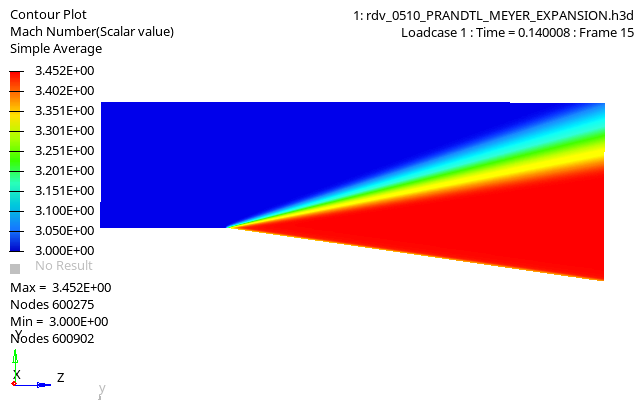
図 5. Mach Number Contour of Fluid Domain

図 6. Density Contour of Fluid Domain
Values of all thermodynamics quantities (pressure, mass density, etc.) in the final state after the expansion fan can be computed, and the numerical results compared to analytical values.
Analytical Analysis

図 7. Deflection of a Supersonic Flow through an Expansion Fan
| Initial State | Final State | |
|---|---|---|
| Mach number | 3 | 3.4519 |
| Pressure [MPa] | 0.180 | 0.0516 |
| Mass density | 1.225E-06 | 7.6337E-07 |
Results Comparison with Analytical Values
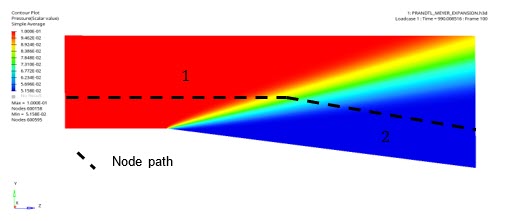
図 8. Two Possible Node Paths Going Through Every State of the Flow
To draw node paths, the elemental results visible on the animation have to be averaged at the nodes, using the averaging method simple in HyperView.
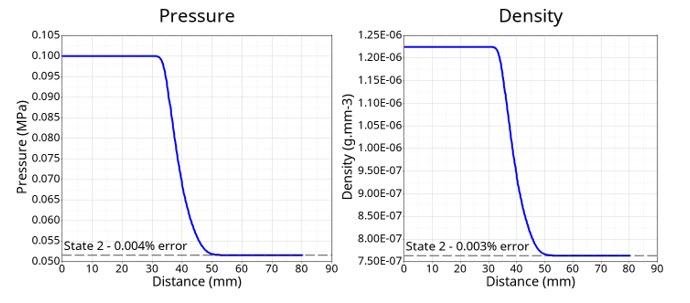
図 9. Pressure and Mass Density Spatial Profile in Steady State. with the value of the relative error to the analytical value
| Values | Analytical | Simulation | Percent Error |
|---|---|---|---|
| Mach number | 3.4519 | 3.4518 | 0.004 |
| Pressure [MPa] | 0.05157 | 0.05158 | 0.004 |
| Mass density | 7.6337E-07 | 7.6334E-07 | 0.003 |
Conclusion
Supersonic flow is modeled using a /MAT/LAW6 hydrodynamic fluid law with an ideal gas equation of state (/EOS/IDEAL-GAS). This material is then referenced by the multi-fluid material /MAT/LAW151 (MULTIFLUID) which uses the finite volume solver. An expansion fan forms as the flow goes around a convex corner.
The analytical approach shows a good correlation between theoretical and numerical results.
The expansion process is correctly simulated. The use of the multi-fluid material allows for very accurate modeling of the dynamics of supersonic flows.