OS-V: 0080 Buckling of Shells and Composites with Offset
A test of influence of offset on buckling solution for shells, including composite with offset Z0 and element offset ZOFFS.

Figure 1. FE Model of the Beam with Boundary Conditions and Loadcases
Benchmark Model
Here, you solve several problems to calculate the critical load on different conditions. The model is a simply supported beam of height 1mm, breadth 2mm and length 100mm with one end constrained in all DOFs and an axial load applied on the other end.
- MAT1
- Young's Modulus
- 1 x 106 N/mm2
- Poisson's Ratio
- 0.0
- Density
- 2 kg/mm3
- Thermal Expansion Coefficient
- 1 x 10-4 ºC-1
- Reference Temperature for Thermal Loading
- 300ºC
- Buckling without offset.
- Buckling with moment equivalent to offset.
- Buckling with offset created by a frame.
- Buckling with offset applied through ZOFFS.
- Buckling of composite with non-symmetrical layup.
- Buckling of composite with offset.
- Maximum or critical force
- Modulus of elasticity
- Area moment of inertia (second moment of area)
- Unsupported length of the beam
- Column effective length factor (for one end fixed and the other end free, =2)
Results

Figure 2. First Four Buckling Eigenvalues for Non-offset (z0 = -0.5)
| Quantity | Theoretical | No-offset | Normalized |
|---|---|---|---|
| cr(1) | 4.1123 | 4.1208 | 0.997937 |
| cr(2) | 16.449 | 16.513 | 0.996124 |
| cr(3) | 37.011 | 37.701 | 0.981698 |
| cr(4) | 102.81 | 108.19 | 0.950273 |

Figure 3. First Four Buckling Eigenvalues for Non-offset + Moment . (the effect of offset is simulated by adding a moment at the end of the beam)
| Quantity | Theoretical | No-offset + Moment | Normalized |
|---|---|---|---|
| cr(1) | 4.1123 | 4.1208 | 0.997937 |
| cr(2) | 16.449 | 16.513 | 0.996124 |
| cr(3) | 37.011 | 37.701 | 0.981698 |
| cr(4) | 102.81 | 108.19 | 0.950273 |

Figure 4. First Four Buckling Eigenvalues for C-Frame. (the effect of offset is simulated by creating a C-shaped frame)
| Quantity | Theoretical | C-Frame | Normalized |
|---|---|---|---|
| cr(1) | 4.1123 | 4.1208 | 0.997937 |
| cr(2) | 16.449 | 16.513 | 0.996124 |
| cr (3) | 37.011 | 37.700 | 0.981724 |
| cr(4) | 102.81 | 108.19 | 0.950273 |

Figure 5. First Four Buckling Eigenvalues for z-offset (Zoffs = -0.5)
| Quantity | Theoretical | ZOFFS | Normalized |
|---|---|---|---|
| cr(1) | 4.1123 | 4.1208 | 0.997937 |
| cr(2) | 16.449 | 16.513 | 0.996124 |
| cr(3) | 37.011 | 37.700 | 0.981724 |
| cr(4) | 102.81 | 108.19 | 0.950273 |
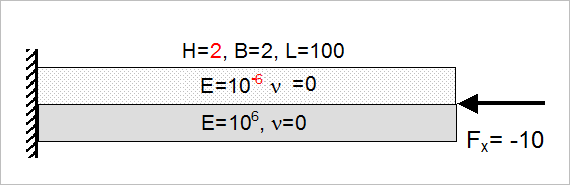
Figure 6. First Four Buckling Eigenvalues for Non-symmetric Layup . (since the top layer is very weak, the load is applied to the “strong” layer with an offset of 0.5)
| Quantity | Theoretical | Non-symmetric Layup | Normalized |
|---|---|---|---|
| cr(1) | 4.1123 | 4.1203 | 0.998058 |
| cr(2) | 16.449 | 16.510 | 0.996305 |
| cr(3) | 37.011 | 37.663 | 0.982689 |
| cr(4) | 102.81 | 107.89 | 0.952915 |

Figure 7. First Four Buckling Eigenvalues for Composites with Offset (z0 = -1)
| Quantity | Theoretical | Offset Composite | Normalized |
|---|---|---|---|
| cr(1) | 4.1123 | 4.1203 | 0.998058 |
| cr(2) | 16.449 | 16.510 | 0.996305 |
| cr(3) | 37.011 | 37.663 | 0.982689 |
| cr(4) | 102.81 | 107.89 | 0.952915 |
Model Files
Refer to Access the Model Files to download the required model file(s).
The model files used in this problem include:
- s100comp_buckl.fem
- s100compmom_buckl.fem
- s100comp_frame_buckl.fem
- s100comp_buckl_zoffs.fem
- s100comp2ply_buckl.fem
- s100compoffs_buckl.fem