RD-E: 1900 Wave Propagation
Elastic wave propagation on a half-space subjected to a vertically-distributed load.
- Lagrangian formulation
- ALE (Arbitrary Lagrangian Eulerian) formulation.

Figure 1.
The domain subjected to the vertical impulse load undergoes an elastic material law process. The generated shock wave is composed of a longitudinal wave and a shear wave. Results are indicated in 0.77 ms, for which the longitudinal wave is predicted to reach the lower boundary of the domain. In order to ensure an accurate wave expansion, an infinite domain is modeled using a non-reflective frontiers (NRF) material law available in the ALE formulation.
Options and Keywords Used
- Bi-dimensional analysis (/ANALY), quad and
general solid
A bi-dimensional problem is considered. The flag N2D3D defined in /ANALY is set to 2. The 2D analysis defines the X-axis as the plane strain direction.
- Impulse load, shock wave propagation, longitudinal and shear waves
- ALE and Lagrangian modeling
- Non-reflective frontiers (NRF) material and infinite domain
- ALE material formulation (/ALE/MAT)
- Concentrated load (/CLOAD)The applied vertical pulse is a concentrated load (/CLOAD) in the form of a sinusoidal function having an amplitude GPa and a time period of .
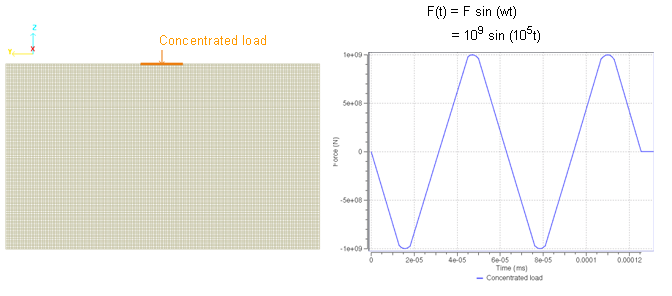
Figure 2. Variation of the Impulse Load Over Time - Function (/FUNCT)
- Non-reflective frontiers (NRF) material LAW11 (/MAT/LAW11 (BOUND))
Figure 3. Fixed Sides
The limitation of this approach is the reflection on the domain's boundaries. Simulation results are shown for the point in time prior to the shock hitting the low side (< 0.77 ms).
- Material Properties
- Initial density
- 2842 kg.m3
- Characteristic length
- 0.0632m
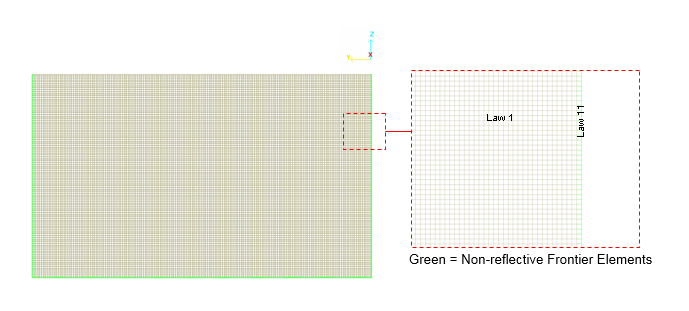
Figure 4. Infinite Domain Modeled by the Non-reflective Frontiers (NRF) Material LAW11 (TYPE3)
The materials have to be declared ALE using /ALE/MAT in the input desk.
Input Files
Refer to Access the Model Files to download the required model file(s).
Model Description
Units: m, s, Kg, N, Pa.
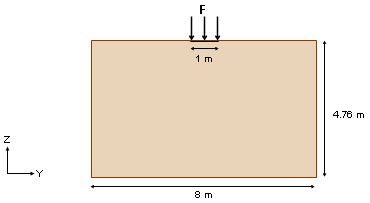
Figure 5. Problem Data
- Material Properties
- Initial density
- 2842 kg.m-3
- Young's modulus
- 73 GPa
- Poisson ratio
- 0.33
The expansion process of the shock wave is comprised of the longitudinal and shear waves.
Based on these material properties, the propagation speed of longitudinal waves in the material correspond to 6169.1 m.s-1 and 3107.5 m.s-1 for shear waves. Thus, the longitudinal waves should reach the lower boundary of the domain in about 0.77 ms.
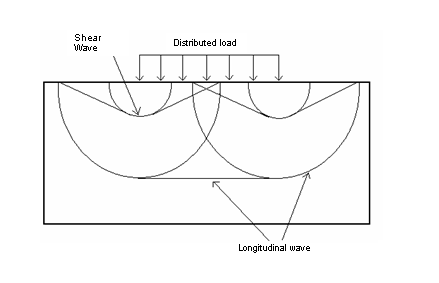
Figure 6. Longitudinal and Shear Waves Comprising the Wave Pattern
The impulse load is described by the sinusoidal function:
Model Method
The part is modeled using a regular mesh with 19080 QUAD elements (44.9 mm x 44.4 mm with =63.15 mm).

Figure 7. Mesh of the Bi-dimensional Domain
Results
Comparison of Lagrangian and ALE Results with the Analytical Solution
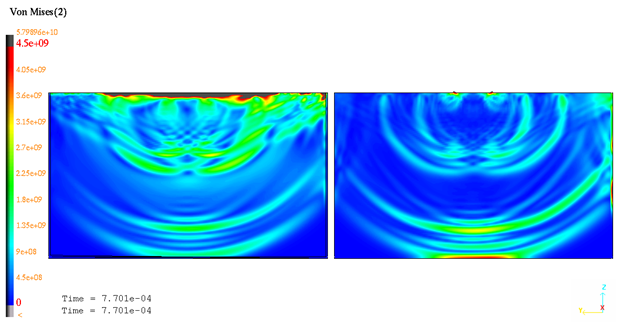
Figure 8. von Mises isovalues at t=0.77 ms
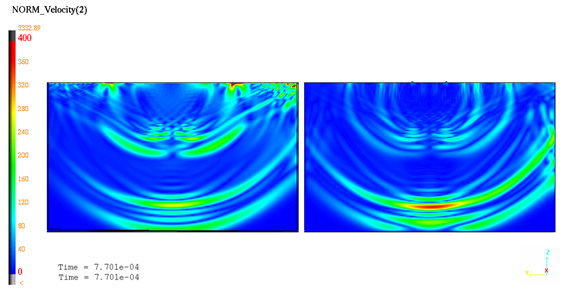
Figure 9. Velocity isovalues at t=0.77 ms
The shock wave propagation is well predicted. Simulation results obtained at t=0.77ms corroborate the analytical solution: Longitudinal and shear waves.
Lagrangian Results
Wave Pattern
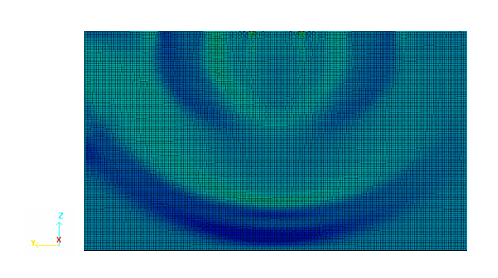
Figure 10. Wave Pattern in Domain at t=0.77 ms
Vertical Displacement
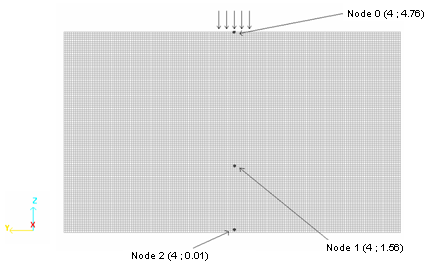
Figure 11. Nodes Saved in Time History
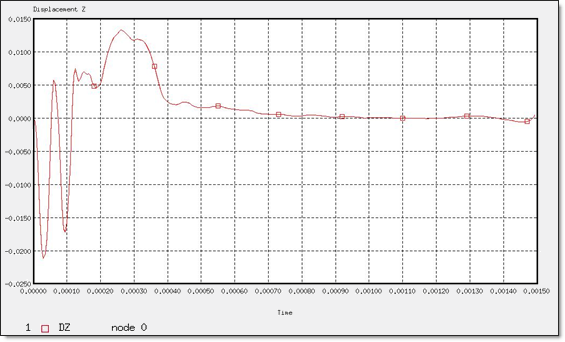
Figure 12. Z-displacement of "Node 0"
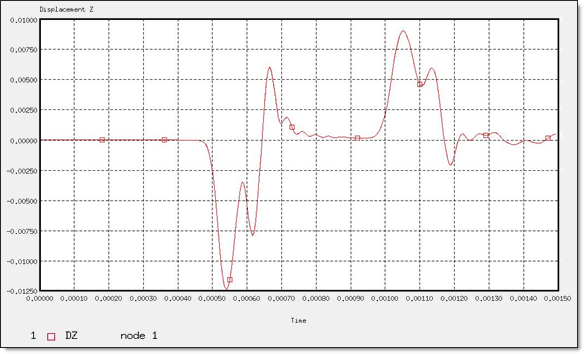
Figure 13. Z-displacement of "Node 1"
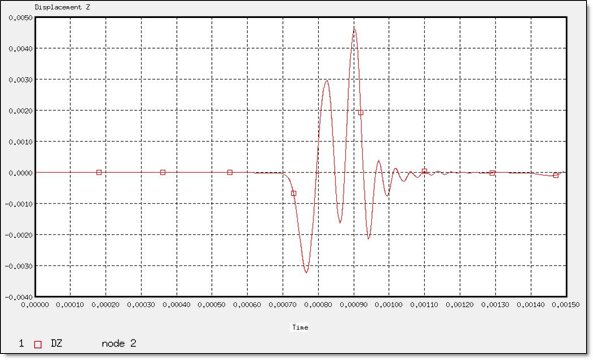
Figure 14. Z-displacement of "node 2"
Horizontal Displacement
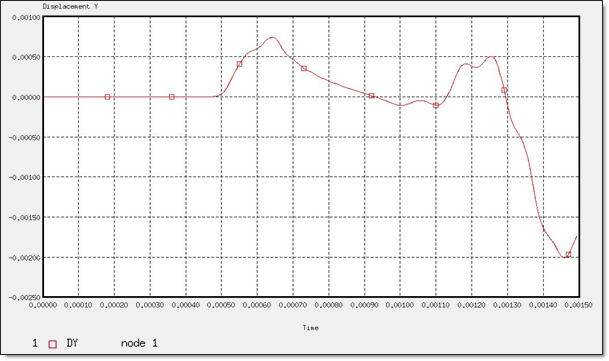
Figure 15. Y-displacement of "node 0"
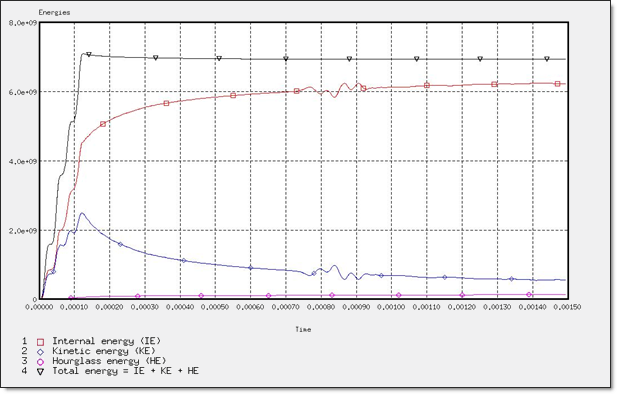
Figure 16. Global Energy Assessment
ALE Results
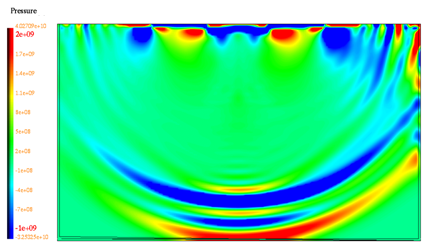
Figure 17. Pressure isovalues at time t=0.77 ms
Conclusion
The wave propagation in a finite domain is studied using Lagrangian and ALE approaches. The Lagrangian formulation does not allow an infinite domain to be defined. Reflections of the longitudinal and shear waves against boundaries restrict simulation in terms of time (t < 0.77 ms). The ALE approach allows you to model an infinite domain by defining the non-reflective frontiers (NRF) material (LAW11 - TYPE3) on the limits. Such specific modeling minimizes the reflection of the expansion wave.
The bi-dimensional analysis illustrates a planar propagation. An accurate representation of the wave pattern is obtained and the simulation results are in a closed agreement with the analytical solution.