/MAT/LAW57 (BARLAT3)

Block Format Keyword This law describes plasticity hardening by a user-defined function and can be used only with shell elements.

This is an elasto-plastic orthotropic law for modeling anisotropic materials in forming processes especially aluminum alloys. This material law must be used with property set type /PROP/TYPE9 (SH_ORTH) or /PROP/TYPE10 (SH_COMP).

Format

(1)	(3)	(5)	(7)	(9)
/MAT/LAW57/`mat_ID`/`unit_ID` or /MAT/BARLAT3/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$ $ρ_{i}$
`E`	$ν$ $ν$
`fct_ID`_E	`E`_inf	`C`_E
`r`₀₀	`r`₄₅	`r`₉₀	`C`_hard	`m`
$ε_{p}^{m a x}$ $ε_{p}^{m a x}$	$ε_{t}$ $ε_{t}$	$ε_{m}$ $ε_{m}$	`F`_cut	`F`_smooth

Repeat the next line for each plasticity function

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
`fct_ID`_i		`Fscale`_i		${\dot{ε}}_{i}$ ${\dot{ε}}_{i}$

Definition

Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	Unit Identifier. (Integer, maximum 10 digits)
`mat_title`	Material title. (Character, maximum 100 characters)
$ρ_{i}$ $ρ_{i}$	Initial density. (Real)	$[\frac{kg}{m^{3}}]$ $[\frac{kg}{m^{3}}]$
`E`	Young's modulus. (Real)	$[Pa]$ $[Pa]$
$ν$ $ν$	Poisson's ratio. (Real)
`fct_ID`_E	Function identifier for the scale factor of Young's modulus, when Young's modulus is function of the plastic strain. 11 Default = 0: in this case the evolution of Young's modulus depends on `E`_inf and `C`_E. (Integer)
`E`_inf	Saturated Young's modulus for infinitive plastic strain. (Real)
`C`_E	Parameter for Young's modulus evolution. (Real)
`r`₀₀	Lankford parameter 0 degree. Default = 1.0 (Real)
`r`₄₅	Lankford parameter 45 degrees. Default = 1.0 (Real)
`r`₉₀	Lankford parameter 90 degrees. Default = 1.0 (Real)
`C`_hard	Hardening coefficient. = 0 Hardening is full isotropic model. = 1 Hardening uses the kinematic Prager-Ziegler model. = between 0 and 1 Hardening is interpolated between the two models. (Real)
`m`	Barlat parameter. = 6.0 (Default) For Body Centered Cubic (BCC) material. = 8.0 For Face Centered Cubic (FCC) material. (Real)
$ε_{p}^{m a x}$ $ε_{p}^{m a x}$	Failure plastic strain. Default = 1.0 x 10³⁰ (Real)
$ε_{t}$ $ε_{t}$	Tensile failure strain at which stress starts to reduce. Default = 1.0 x 10³⁰ (Real)
$ε_{m}$ $ε_{m}$	Maximum tensile failure damage strain at which the stress in element is set to zero. Default = 2.0 x 10³⁰ (Real)
`F`_cut	Cutoff frequency for the strain rate filtering. Default = 10000 Hz (Real)	$[Hz]$ $[Hz]$
`F`_smooth	Smooth strain rate option flag. = 0 (Default) No strain rate smoothing. = 1 Strain rate smoothing active. (Integer)
`fct_ID`_i	Plasticity curves `i`^th function identifier. (Integer)
`Fscale`_i	Scale factor for `i`^th function. Default set to 1.0 (Real)
${\dot{ε}}_{i}$ ${\dot{ε}}_{i}$	Strain rate for `i`^th function. (Real)	$[\frac{1}{s}]$ $[\frac{1}{s}]$

▸Example (Steel)

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
                   g                  mm                  ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW57/1/1
Steel
#              RHO_I
                .008                   
#                  E                  NU
              206000                  .3
#FUNCT_IDE                          EINF                  CE
         0                             0                   0
#                r00                 r45                 r90              C_hard                   m
                1.79                1.51                2.27                   0                   0
#           EPSP_max               EPS_T               EPS_M                Fcut  Fsmooth
                   0                   0                   0                  10        1
# funct_ID                      Fscale_i               EPS_i
         5                             0                   0                                        
         5                             0                   1                                        
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  3. FUNCTIONS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/5
function_5
#                  X                   Y
                   0                 157                                                            
                  .1                 320                                                            
                  .5                 480                                                            
                 1.2                 600                                                            
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Comments

The anisotopic yield criteria F for plane stress is defined by:(1)
$F = a {| K_{1} + K_{2} |}^{m} + a {| K_{1} - K_{2} |}^{m} + c {| 2 K_{2} |}^{m} - 2 {σ_{y}}^{m} = 0$ $F = a {| K_{1} + K_{2} |}^{m} + a {| K_{1} - K_{2} |}^{m} + c {| 2 K_{2} |}^{m} - 2 {σ_{y}}^{m} = 0$

Where,

$σ_{y}$ $σ_{y}$ is the yield stress

$K_{1} = \frac{σ_{x x} + h σ_{y y}}{2}$ $K_{1} = \frac{σ_{x x} + h σ_{y y}}{2}$ and $K_{2} = \sqrt{{(\frac{σ_{x x} - h σ_{y y}}{2})}^{2} + p^{2} σ_{x y}^{2}}$ $K_{2} = \sqrt{{(\frac{σ_{x x} - h σ_{y y}}{2})}^{2} + p^{2} σ_{x y}^{2}}$
Angles for Lankford parameters are defined with respect to orthotropic direction 1. The material constants a, c, h, and p are obtained from the three Lankford parameters:(2)
$\begin{array}{l} a = 2 - 2 \sqrt{\frac{r_{00}}{1 + r_{00}}} \sqrt{\frac{r_{90}}{1 + r_{90}}} \\ c = 2 - a \\ h = \sqrt{\frac{r_{00}}{1 + r_{00}}} \sqrt{\frac{1 + r_{90}}{r_{90}}} \end{array}$ $\begin{array}{l} a = 2 - 2 \sqrt{\frac{r_{00}}{1 + r_{00}}} \sqrt{\frac{r_{90}}{1 + r_{90}}} \\ c = 2 - a \\ h = \sqrt{\frac{r_{00}}{1 + r_{00}}} \sqrt{\frac{1 + r_{90}}{r_{90}}} \end{array}$

Material constant p is calculated by solving:(3)
$\frac{2 m \cdot σ_{y}^{m}}{(\frac{\partial F}{\partial σ_{x x}} + \frac{\partial F}{\partial σ_{y y}}) σ_{45}} - 1 - r_{45} = 0$ $\frac{2 m \cdot σ_{y}^{m}}{(\frac{\partial F}{\partial σ_{x x}} + \frac{\partial F}{\partial σ_{y y}}) σ_{45}} - 1 - r_{45} = 0$
If the last point of the first (static) function equals 0 in stress, the default value of $ε_{p}^{m a x}$ $ε_{p}^{m a x}$ is set to the corresponding value of $ε_{p}$ $ε_{p}$ .
If $ε_{p}$ $ε_{p}$ (plastic strain) reaches $ε_{p}^{\max}$ $ε_{p}^{\max}$ , in one integration point, the corresponding shell element is deleted.
If the largest principal strain $ε_{1} > ε_{t}$ $ε_{1} > ε_{t}$ , the stress is reduced using the following relation:(4)
$σ = σ (\frac{ε_{m} - ε_{1}}{ε_{m} - ε_{t}})$ $σ = σ (\frac{ε_{m} - ε_{1}}{ε_{m} - ε_{t}})$
If $ε_{1} > ε_{m}$ $ε_{1} > ε_{m}$ , the stress is reduced to 0 (but the element is not deleted).
The maximum number of curves is 10.
If $\dot{ε} \leq {\dot{ε}}_{n}$ $\dot{ε} \leq {\dot{ε}}_{n}$ , the yield is interpolated between f_n and f_n-1.
If $\dot{ε} \leq {\dot{ε}}_{1}$ $\dot{ε} \leq {\dot{ε}}_{1}$ , function f₁ is used.
Above ${\dot{ε}}_{\max}$ ${\dot{ε}}_{\max}$ , yield is extrapolated.

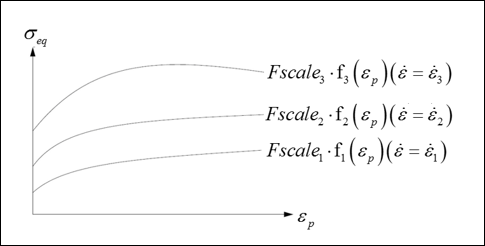
Figure 1.
The evolution of Young's modulus:
- If fct_ID_E > 0, the curve defines a scale factor for Young's modulus evolution with equivalent plastic strain, which means the Young's modulus is scaled by the function $f ({\bar{ε}}_{p})$ $f ({\bar{ε}}_{p})$ :(5)
  $E (t) = E \cdot f ({\bar{ε}}_{p})$ $E (t) = E \cdot f ({\bar{ε}}_{p})$
  
  The initial value of the scale factor should be equal to 1 and it decreases.
- If fct_ID_E = 0, the Young's modulus is calculated as:(6)
  $E (t) = E - (E - E_{i n f}) [1 - \exp (- C_{E} {\bar{ε}}_{p})]$ $E (t) = E - (E - E_{i n f}) [1 - \exp (- C_{E} {\bar{ε}}_{p})]$
  
  Where, E and E_inf are respectively the initial and asymptotic value of Young's modulus, and ${\bar{ε}}_{p}$ ${\bar{ε}}_{p}$ is the accumulated equivalent plastic strain.
  
  Note: If fct_ID_E = 0 and C_E = 0, Young's modulus, E is kept constant.
The parameters F_smooth and F_cut allows you to enable a strain-rate filtering. Three cases can be set:
- If F_smooth = 0 and F_cut = 0.0, the strain-rate filtering is turned off.
- If F_smooth = 1 and F_cut = 0.0, the strain-rate filtering uses a default cutoff frequency of 10 kHz.
- If F_cut ≠ 0, F_smooth is automatically set to 1 and the strain-rate filtering uses the cutoff frequency given by you.