/MAT/LAW53 (TSAI_TAB)

Block Format Keyword Describes the law that is a uni-directional orthotropic elasto-plastic law and is only used with solid elements.

Format

(1)	(2)	(3)	(4)	(5)	(7)	(9)
/MAT/LAW53/`mat_ID`/`unit_ID` or /MAT/TSAI_TAB/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$
`E`₁₁		`E`₂₂
`G`₁₂		`G`₂₃
`fct_ID`₁₁	`fct_ID`₂₂	`fct_ID`₁₂	`fct_ID`₂₃	`fct_ID`₄₅
`Fscale`₁₁		`Fscale`₂₂		`Fscale`₁₂	`Fscale`₂₃	`Fscale`₄₅

Definition

Field	Contents	SI Unit Example
`mat_ID`	Material identifier (Integer, maximum 10 digits)
`unit_ID`	Unit Identifier (Integer, maximum 10 digits)
`mat_title`	Material title (Character, maximum 100 characters)
$ρ_{i}$	Initial density (Real)	$[\frac{kg}{m^{3}}]$
`E`₁₁	Young's modulus (Real)	$[Pa]$
`E`₂₂	Young's modulus (Real)	$[Pa]$
`G`₁₂	Shear modulus (Real)	$[Pa]$
`G`₂₃	Shear modulus (Real)	$[Pa]$
`fct_ID`₁₁	Yield stress function identifier in direction 11 (Integer)
`fct_ID`₂₂	Yield stress function identifier in direction 22 (Integer)
`fct_ID`₁₂	Yield stress function identifier in direction 12 (Integer)
`fct_ID`₂₃	Yield stress function identifier in direction 23 (Integer)
`fct_ID`₄₅	Yield stress function identifier in direction 45 (Integer)
`Fscale`₁₁	Scale factor for yield function 11 Default = 1.0 (Real)	$[Pa]$
`Fscale`₂₂	Scale factor for yield function 22 Default = 1.0 (Real)	$[Pa]$
`Fscale`₁₂	Scale factor for yield function 12 Default = 1.0 (Real)	$[Pa]$
`Fscale`₂₃	Scale factor for yield function 23 Default = 1.0 (Real)	$[Pa]$
`Fscale`₄₅	Scale factor for yield function 45 Default = 1.0 (Real)	$[Pa]$

Example (Plastic)

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
                 Mg                  mm                   s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW53/1/1
plastic
#              RHO_I
               2E-10
#                E11                 E22
                 200                 200
#                G12                 G23
                 100                 100
# fct_ID11  fct_ID22  fct_ID12  fct_ID23  fct_ID45
         1         1         3         4         5
#           Fscale11            Fscale22            Fscale12            Fscale23            Fscale45
                   0                   0                   0                   0                   0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  3. FUNCTIONS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/1
function_1
#                  X                   Y
                   0                 200                                                           
                  .1                 200                                                           
                 .11                 100                                                           
                  .5                 100                                                           
                 1.5               20000                                                           
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2
function_2
#                  X                   Y
                   0                   1                                                           
               10000                   1                                                           
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/3
function_3
#                  X                   Y
                   0                 200                                                           
                  .1                 200                                                           
                 .11                 100                                                           
                  .5                 100                                                           
                 1.5               20000                                                           
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/4
function_4
#                  X                   Y
                   0                 200                                                           
                  .5                 200                                                           
                 1.5               20000                                                           
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/5
function_5
#                  X                   Y
                   0                 100                                                           
                  .5                 100                                                           
                 1.5               20000                                                           
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Comments

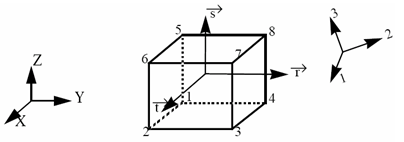
Orthotropic reference frame (1, 2, and 3) is defined in the appropriate property set of each finite element.
For SOLID property set (/PROP/TYPE14), the global frame is used if I_solid = 1 or 2.

Figure 1.
The global frame is ( $X$ , $Y$ , and $Z$ ).

The local frame is (

t

r

, and

s

$σ_{11} = E_{11} ε_{11}$	$σ_{12} = G_{12} ε_{12}$
$σ_{22} = E_{22} ε_{22}$	$σ_{23} = G_{23} ε_{23}$
$σ_{33} = E_{33} ε_{33}$	$σ_{13} = G_{13} ε_{13}$

The law is othotropic, E₃₃ = E₂₂ and G₁₃ = G₁₂.
The yield surface is Tsai-Wu yield criteria:(1)
$\begin{array}{l} F = F_{1} σ_{11} + F_{2} σ_{22} + F_{2} σ_{33} + F_{11} σ_{11}^{2} + F_{22} σ_{22}^{2} + F_{22} σ_{33}^{2} \\ + F_{44} σ_{12}^{2} + F_{55} σ_{23}^{2} + F_{44} σ_{13}^{2} + 2 F_{12} σ_{11} σ_{22} + 2 F_{23} σ_{22} σ_{33} \\ + 2 F_{12} σ_{11} σ_{33} \end{array}$

with (2)
$\begin{matrix} F_{1} = - \frac{1}{σ_{1 y}^{c}} + \frac{1}{σ_{1 y}^{t}}; & F_{2} = - \frac{1}{σ_{2 y}^{c}} + \frac{1}{σ_{2 y}^{t}} \end{matrix}$
(3)
$\begin{matrix} F_{11} = \frac{1}{σ_{1 y}^{c} σ_{1 y}^{t}}; & F_{22} = \frac{1}{σ_{2 y}^{c} σ_{2 y}^{t}}; & F_{44} = \frac{1}{σ_{4 y}^{c} σ_{4 y}^{t}}; & F_{55} = \frac{1}{σ_{5 y}^{c} σ_{5 y}^{t}} \end{matrix}$
(4)
$\begin{matrix} F_{12} = - \frac{1}{2} \sqrt{F_{11} F_{22}}; & F_{23} = - \frac{1}{2} F_{22} \end{matrix}$

The parameters: $σ_{1 y}^{c}, σ_{1 y}^{t}, σ_{2 y}^{c}, σ_{2 y}^{t}, σ_{4 y}^{c}, σ_{4 y}^{t}, σ_{5 y}^{c}, σ_{5 y}^{t}$ are variable and introduced by yield function.
If fct_ID₄₅ ≠ 0,(5)
$F_{12} = \frac{2}{σ_{45 y}^{2}} - \frac{1}{2} (F_{11} + F_{22} + F_{44}) + \frac{F_{1} + F_{2}}{σ_{45 y}^{c}}$