2D curve: Integrale

Introduction

The user can represent the result of integrals calculated from functions of spatial quantities or input/output parameters in the form of curves.

Operation

The curves of integrals are created as follows:

Stage	Description
1	The Integral of a 2D curve command is applied to an elementary curve or a set of elementary curves of the 2D curve entity.
2	The function representing the integral of each analyzed curve is constructed by the calculation of the integral at each point of the interval of the curve definition.
3	The new elementary curves are added to the already available curves of the 2D curve entity.

Principle

The integral is calculated starting from the function represented by the analyzed curve. The integration is performed following the trapezoid rule.

Given a curve representing the function f(x), the calculation of the integral in each point is carried out as follows:

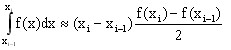
The number of points of the curve representing the integral is the same as that of the initial curve.

The ordinate of the first point of the curve representing the integral is always nul.

The abscissa values a and b in the integral must be strictly increasing ones (b>a).

Trapezoide method: reminder

The trapezoid rule is a method to numerically calculate the integral: .

The principle of the trapezoid rule consists in approximating the region under the graph of the function f(x) by a trapezoid and calculating its area:

To calculate the integral more accurately, the interval of integration a,b is split into n smaller subintervals and the method is applied to each of them.

Compute the integral of a 2D curve

To compute (and display) the integral of a 2D curve, see following steps:

Etape	Action
1	In the menu Curve > 2D curve (…): click on Integral of a 2D curve
→	A selection box opens
2	In the selection dialog, choose the 2D curve entity
3	In the Integral of a 2D curve dialog, choose the elementary curve(s) to be analyzed
→	The curves of the integral are calculated and displayed in the 2D curve sheet.