ランダム応答疲労解析

ランダム荷重下の構造の疲労寿命の検討。

ランダム応答解析から得られるパワースペクトル密度（PSD）は、サイクル数対応力範囲の確率密度関数を生成するために使用される、モーメント（ $m_{n}$ ）の計算に使用されます。

HyperLifeでランダム応答疲労解析を実行する方法は2種類あります：

Random Fatigueで既に利用可能であるPSD応力を使用
HyperLifeで周波数応答解析とパワースペクトル密度関数 vs 周波数から生成されたPSD応力を使用

ランダム疲労ですでに利用可能であるPSD応力

PSDモーメントは、次に示すように、ランダム応答解析から生成される応力PSDに基づいて計算されます。

入力

ランダム応答疲労を計算。

パワースペクトル密度（PSD）モーメント

PSDモーメント（

m_{n}

）は、次に示すように、ランダム応答解析から生成される応力PSDに基づいて計算されます。

Figure 1. PSDモーメントの計算

モーメントは、次の式に基づいて計算されます：(1)

m_{n} = \sum_{k = 1}^{N} f_{k}^{n} G_{k} δ f

ここで、

$f_{k}$: 周波数の値
$G_{k}$: 右記の周波数でのPSD応答値； $f_{k}$

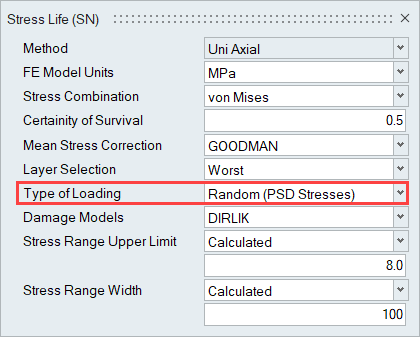
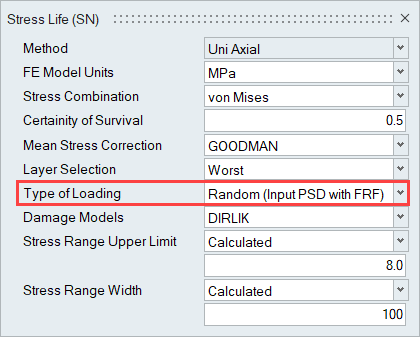
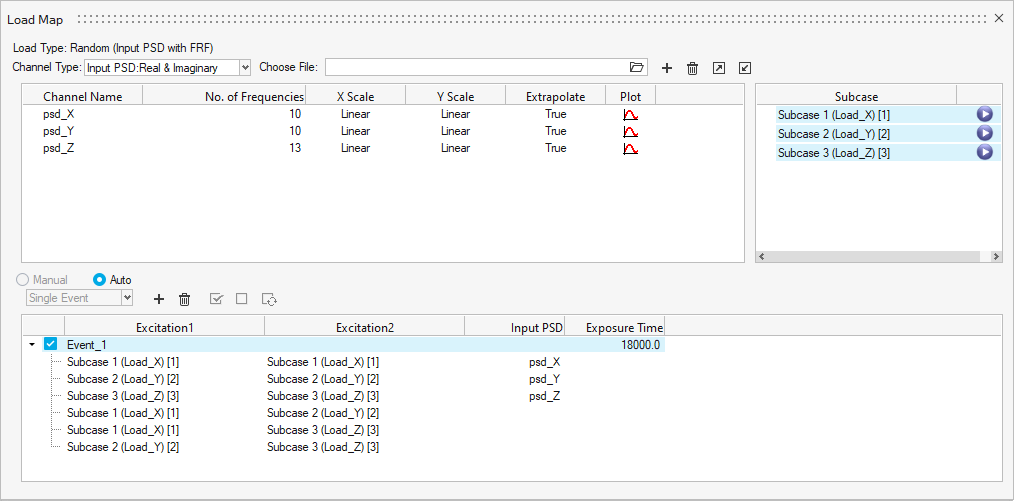
$m_{0}$ の安定は、PARAM, CHKM0, YES設定によってチェックされます。周波数間隔をさらに細分化する必要がある場合は、警告が表示されます。

応力範囲の存在確率の計算

各binセクション内の最初と最後の応力範囲値の間に応力範囲が存在する確率の計算は、ユーザーが定義します。

$(Δ S_{i} - δ S / 2)$ と $(Δ S_{i} + δ S / 2)$ の間に応力範囲が存在する確率 $P (Δ S_{i})$ は、 $P (Δ S_{i}) = p_{i} δ S$ となります。

確率密度関数（応力範囲に対するサイクル数の確率密度）

上記のとおり計算されたPSDモーメントは、応力範囲の確率密度関数 $f (m_{n})$ の生成に使用されます。この関数は、SN FatigueモジュールのRandom Response Fatigueセクション内で指定された損傷モデルに基づきます。現在、DIRLIK、LALANNE、NARROWおよびTHREEオプションを損傷モデルの定義に使用できます。

DIRLIK（デフォルトの損傷モデル）：

DIRLIKは、確率密度関数の決定への閉じたフォームの解を公準化します：(2)

p (S) = \frac{\frac{D_{1}}{Q} e^{\frac{- Z}{Q}} + \frac{D_{2} Z}{R^{2}} e^{\frac{- Z^{2}}{2 R^{2}}} + D_{3} Z e^{\frac{- Z^{2}}{2}}}{2 \sqrt{m_{0}}}

ここで、

$D_{1} = \frac{2 (x_{m} - γ^{2})}{1 + γ^{2}}$
$D_{2} = \frac{1 - γ - D_{1} + D_{1}^{2}}{1 - R}$
$D_{3} = 1 - D_{1} - D_{2}$
$Z = \frac{S}{2 \sqrt{m_{0}}}$
$Q = \frac{1.25 (γ - D_{3} - D_{2} R)}{D_{1}}$
$R = \frac{γ - x_{m} - D_{1}^{2}}{1 - γ - D_{1} + D_{1}^{2}}$
$γ = \frac{m_{2}}{\sqrt{m_{0} m_{4}}}$: 不規則性要因
$x_{m} = \frac{m_{1}}{m_{0}} \sqrt{\frac{m_{2}}{m_{4}}}$
$S$: 応力範囲

LALANNE：

LALANNEランダム疲労損傷モデルは次のように確率密度関数を示します： (3)

p (S) = \frac{1}{\sqrt{m_{0}}} \frac{\sqrt{1 - γ^{2}}}{\sqrt{2 π}} e^{\frac{- S^{2}}{8 m_{0} (1 - γ^{2})}} + \frac{S γ}{4 \sqrt{m_{0}}} (1 + e r f (\frac{S γ}{2 \sqrt{2 m_{0} (1 - γ^{2})}}))

ここで、

$γ = \frac{m_{2}}{\sqrt{m_{0} m_{4}}}$: 不規則性要因
$S$: 応力範囲

NARROW：

狭帯域ランダム疲労損傷モデルは、次の確率関数を使用します：(4)

p (S) = (\frac{S}{4 m_{0}} e^{- (\frac{S^{2}}{8 m_{0}})})

ここで、 $S$ は応力範囲です。

デフォルトではHyperLifeは、狭帯域にはゼロクロッシングの数（ $n_{z c r o s s} = \sqrt{m_{2} / m_{0}}$ ）をピークの数（ $n_{p e a k s} = \sqrt{m_{4} / m_{2}}$ ）の代わりに使用します。これは、 $m_{4}$ を含んだ数値計算が数値的に不安定に陥ることがあるためです。

THREE：

Steinberg 3-Bandランダム疲労損傷モデルは、次の確率関数を使用します。

他の損傷モデルとは異なり、THREE帯には以下の値が確率です（確率密度ではない）。これは、他のモデルが小文字

P (S)

を使うことに対し、大文字

p (S)

を使うことでも明らかです。THREE損傷モデルでは、下記の確率を直接使用し、

P (S)

に時刻歴全体のゼロクロッシングの総数を掛けることによって計算します（THREE以外の他のモデルの場合、確率密度値はまずDS (bin size)を掛けることで確率を得ます）。(5)

P (S) = {\begin{matrix} 0.683 at 2 \sqrt{m_{0}} \\ 0.271 at 4 \sqrt{m_{0}} \\ 0.043 at 6 \sqrt{m_{0}} \end{matrix}

ここで、 $S$ は応力範囲です。

Figure 2. 確率密度関数（応力範囲に対するサイクル数の確率密度）

確率密度関数は、SN FatigueモジュールのRandom Response Fatigueセクション内で定義されている次のパラメータに基づいて調整できます：

Upper Stress Range (Calculated): 応力範囲の上限を計算します。これは次のように計算されます：応力範囲の上限 = 2*RMS Stress*Upper Stress Range (Calculated) input.RMS応力はランダム応答サブケースから出力されます。対象となる応力範囲は、応力範囲の上限によって制限されます。その上限を上回る応力は、ランダム疲労損傷計算では考慮されません。
Width: Stress Range (Calculated): 確率を計算する応力範囲（DS = $δ S$ の幅を計算します（Figure 2）。デフォルトは100で、最初のbinは0.0から始まり $δ S$ までとなります。応力範囲の幅は、DS = 応力範囲の上限 / Width: Stress Range (Calculated)と計算されます。

応力範囲の存在確率の計算

各binセクション内の最初と最後の応力範囲値の間に応力範囲が存在する確率の計算は、損傷モデルに基づきます。

DIRLIK、LALANNEおよびNARROW損傷モデル

between $(S_{i} - δ S / 2)$ と $(S_{i} + δ S / 2)$ の間に応力範囲が存在する確率 $P (S_{i})$ は、 $P (S_{i}) = p_{i} (S_{i}) δ S$ となります。

THREE損傷モデル

確率は、上で定義された確率関数を用いて直接定義されます。明確にするために、ここで繰り返します。(6)

P (S) = {\begin{matrix} 0.683 at 2 \sqrt{m_{0}} \\ 0.271 at 4 \sqrt{m_{0}} \\ 0.043 at 6 \sqrt{m_{0}} \end{matrix}

ここで、 $S$ は応力範囲です。

THREE損傷モデルについては、binは3つのみです。各応力範囲におけるサイクル数（2*RMS、4*RMS、6*RMS）は、対応する確率をゼロクロッシングの総数に直接掛けることにより計算されます（ゼロクロッシングの数の計算については、以下のセクションを参照のこと）。

損傷モデルの選択

DIRLIK、LALANNE、NARROWおよびTHREEは、SN疲労モジュールのRandom Response Fatigueセクションで選択できます。以下の情報は、HyperLife実行のための損傷モデルの選択のための追加情報です。

これより前のセクションでは、応力のPSDモーメントが対応するモーメントの計算に使用されることが説明されましたが、これを用いて、応力範囲の確率密度関数が決定されます。
DIRLIKおよびLALANNEモデルは、応力範囲スペクトラムのより広範な分布にわたる確率を生成します。したがって、これらのモデルは、入力のランダム信号が、複数の周波数にわたる様々な応力範囲から成る際に使用されるべきです。ゆえに、DIRLIKとLALANNEが使用されている場合、確率密度関数内の情報は、より広範な応力範囲の分布をより良く捕捉します。
応力範囲が、高確率である特定の応力範囲分布と密に関連していることが期待されるランダム信号には、NARROWモデルが適しています。したがって、入力のランダムデータが広範にわたる応力範囲分布を擁さず、分布が主として特定の応力範囲に集中している場合、この特定の応力範囲またはその周辺で最も高確率である応力範囲が期待できるNARROWを選択すべきです。
THREEモデルはNARROWと同様ですが、ランダム信号の分布が1*RMSとの関連に加え、2*RMSおよび3*RMSとの関連が少ないながら含まれていることが前提となっているところが異なります。したがって、入力のランダムデータが主として1*RMS内の応力範囲の周辺に多く見られ、2*RMSおよび3*RMS周りでは少ない場合、THREEを選択すべきです。

ピークおよびゼロクロッシングの数

NARROWおよびTHREE損傷モデルの場合

元の時間領域ランダム荷重での１秒当たりのゼロクロッシングの数（周波数に基づくランダムPSD荷重はここから生成されます）は、次のように決定されます：(7)

n_{z c r o s s} = \sqrt{\frac{m_{2}}{m_{0}}}

DIRLIKおよびLALANNE損傷モデルの場合

元の時間領域ランダム荷重での１秒当たりのピークの数（周波数に基づくランダムPSD荷重はここから生成されます）は、次のように決定されます：(8)

n_{p e a k s} = \sqrt{\frac{m_{4}}{m_{2}}}

ここで、 $m_{n}$ は、パワースペクトル密度（PSD）モーメントで示されるとおり計算される対応するモーメントです。

THREE帯およびNARROW帯のサイクル総数は、次のように計算されます：(9)

N_{T} = n_{z c r o s s} T

DIRLIK, LALANNEおよびNARROW のサイクル総数は、次のように計算されます：

(10)

N_{T} = n_{p e a k s} T

ここで、 $T$ はLoad Mapダイアログでイベントを作成される際のRepeats/Time値

特定の応力範囲のサイクルの合計数

応力範囲

Δ S_{i}

でのサイクルの合計数は、次のように計算されます：(11)

N_{i} = P (S_{i}) N_{T}

疲労寿命と損傷

疲労寿命（破壊までのその材料の特定の応力範囲

S_{i}

のサイクルの最大数）は、次のように、材料SN曲線に基づいて計算されます：(12)

N_{f} (S_{i}) = {(\frac{S_{i}}{S_{f}})}^{\frac{1}{b}}

ランダム荷重の適用からもたらされる合計疲労損傷は、次に基づいて計算されます：(13)

D = \sum_{i = 1}^{N} \frac{N_{i}}{N_{f} (S_{i})}

ゼロでない平均応力をもたらすような荷重による平均応力補正を考慮するには、そのような荷重（通常は重力荷重）から成る静的サブケースを定義します。この静的サブケースは、Load Mapダイアログで作成される疲労イベント内で参照されます。

設定

Randomサブケースを含むFE結果ファイルの読み込み後に、Type of Loading欄をRandom (PSD Stresses)に設定すると、ランダム応答疲労がアクティブになります。ランダム疲労でサポートされている結果のデータ型は、Segalman Von mises PSD応力（応力寿命のみ）またはAbsolute Max Principal PSD応力（応力寿命およびひずみ寿命）です。

ランダム疲労向けにHyperLifeで周波数応答解析とパワースペクトル密度関数荷重 vs 周波数から生成されるPSD応力

PSD応力は、FRF応力と入力PSDを使用して内部的に計算されます。最初に作成された疲労イベントでPSD応力が計算され（ランダム応答解析）、次に、このPSD応力がPSDモーメントの計算に使用されます。

異なる加振（aおよびb）

H_{x a} (f)

および

H_{x b} (f)

が自由度

x

で、それぞれの周波数応答解析荷重ケースが

a

と

b

である場合の複素周波数応答（応力）の場合、自由度

x

の応答のパワースペクトル密度、

S_{x o} (f)

は：(14)

S_{x o} (f) = H_{x a} (f) S_{a b} (f) H_{x b} (f)

ここで、 $S_{a b} (f)$ は２つの（異なる、 $a \neq b$ ）ソースのクロスパワースペクトル密度で、個別ソース $a$ は加振荷重ケース、 $b$ は適用荷重ケースです。この値は複素数であり得ます。

同じ荷重ケース（a）

S_{a} (f)

が個別ソース（荷重ケース

a

のスペクトル密度である場合、荷重ケース

a

による自由度

x

の応答のパワースペクトル密度は：(15)

S_{x o} (f) = {| H_{x a} (f) |}^{2} S_{a} (f)

単一のランダム応答解析における異なる(a,b)荷重ケースと同じ(a,a)荷重ケースの組み合わせ

ランダム応答解析について荷重ケースの組み合わせがある場合、応答の全パワースペクトル密度は、個々のすべての（同じ）荷重ケースとすべての（異なる）クロス荷重ケースによる応答のパワースペクトル密度の和になります。

設定

周波数応答解析サブケースを含むFE結果ファイルの読み込み後に、Type of Loading欄をRandom (Input PSD with FRF)に設定すると、ランダム応答疲労がアクティブになります。

荷重対周波数のパワースペクトル密度が大きさと位相で表される場合は、実数部と虚数部に変換されます。

Load Map:

入力PSDは以下のChannel Typeの選択内容に基づいています。

Input PSD: Real and Imaginary
Input PSD: Magnitude and Phase

イベントは、選択されている周波数応答サブケースの数に基づき、相関を使用して作成されます。インポートされたチャンネル（荷重対周波数の入力パワースペクトル密度）は、各相関に割り当てられます。

Excitation1およびExcitation2は、FRFサブケースの相関を指します。入力PSDは、複素応力のスケーリングに使用されます。入力PSDが大きさと位相の形式である場合は、実数部と虚数部に内部的に変換されます。

次に、PSD応力がすでに利用可能である場合（この章の最初に説明）と同様に、上記のイベントから計算されたPSD応力が疲労の計算に使用されます。