シンプレックス(ネルダーミード法)
シンプレックス(ネルダーミード法)アルゴリズムは、最終的な最適解が、指定した開始点に大きく依存するローカル検索法(山登り検索法)として分類できます。
N次元空間でN+1個の点によって形成される幾何学的図形をシンプレックスと呼びます。シンプレックス法の基本的な概念は、一般的なシンプレックス(各点が単一の組み合わせのパラメータ値を表すシンプレックス)を形成するN+1個の点の位置で結合した目標値を比較して、反復プロセスでこのシンプレックスを最適点に徐々に近付けるというものです。シンプレックスの移動は、鏡像、収縮、および拡張という3つの操作で実現します。
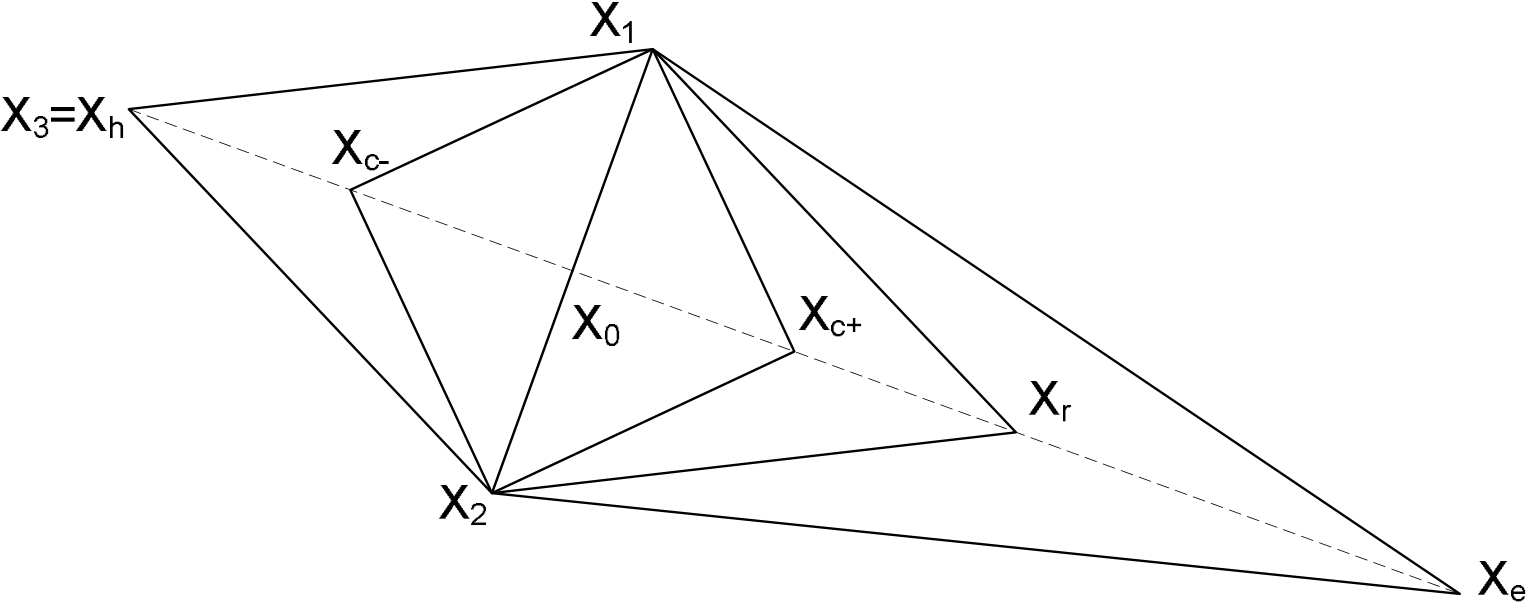
Figure 1. シンプレックス法による鏡像、拡張、および収縮。
鏡像
Figure 1を検討します。初期シンプレックスの点のうち、適合度が最も低い点がXhであるとすると、このシンプレックスにある他の点(X1とX2)によって決まる軸を中心にして点Xhを鏡像移動することで得られる点Xrで、(最適化目標に従って評価した場合に)より高い適合度の値が得られることが考えられます。その場合は、このシンプレックスから点Xhを除外して、新しい点Xrを取り入れることで、新しいシンプレックスを作成できます。Figure 1は、このプロセスを示しています。ここでは、X1、X2、およびXrの各点によって新しいシンプレックスを形成しています。シンプレックスの移動方向は必ず、最悪の結果から離れる方向であることから、必ず好ましい方向への移動になります。パラメータの範囲で定義した空間の範囲で、グローバル目標関数が急勾配の谷状に変化しない場合は、鏡像プロセスを繰り返し適用すると、最適解の一般的な方向にジグザグの移動経路が伸びていきます。
拡張
鏡像プロセスで、このシンプレックスにあるどの点よりも高い適合度の点Xr(新しい最適点)が見つかった場合は、X0からXrの方向に沿って移動することで、さらに優れた最良の適合値が得られることが考えられます。したがって、XrからXeへの拡張を実行します。
Xeで評価した適合度がXrの適合度より高い場合、その拡張には成果があるので、XhをXeに置き換えて鏡像プロセスを再開します。Xeで評価した適合度が低くなった場合、その拡張は失敗であり、XhをXr(直前の鏡像操作で特定した点)に置き換えて鏡像プロセスを続行します。
収縮
鏡像プロセスで、現在のシンプレックスの中で適合度が2番目に高い点(Xnh)よりも優れた適合度の点Xrが見つかった場合は、収縮操作を実行します。
収縮プロセスで、このシンプレックスにあるどの点よりも高い適合度の点Xcが得られた場合、その収縮には成果があるので、XhをXcに置き換えて鏡像プロセスを続行します。収縮プロセスで、適合度が低下した点Xcが得られた場合、その収縮プロセスは失敗であり、シンプレックスにあるすべての点を内部係数でスケーリングすることで、シンプレックスの基線を短くして鏡像プロセスを再開します。
| 目的関数 | 操作 |
|---|---|
| F(Xr) < F(Xl) | 拡張 |
| F(Xl) ≤ F(Xr) < F(Xnh) | 鏡像 |
| F(Xnh) ≤ F(Xr) < F(Xh) | 正の収縮 |
| F(Xh) ≤ F(Xr) | 負の収縮 |
エラー処理と終了
- Fekoソルバーの最大実行回数に達したとき
- シンプレックスの頂点間の標準偏差が十分に小さくなったとき
- シンプレックスの基線が十分に小さくなったとき
- 最適化目標に達したとき
テキストログ
最適化では、OPTFEKOによって最適化プロセスのテキストログがプロジェクトの.logファイルに保持されます。このファイルの構造は主に最適化手法によって決まります。
========================= L O G - FILE - OPTFEKO =========================
Version: 13.22 of 2007-05-08
Date: 2007-06-06 16:45:43
File: test
OPTIMISATION WITH ALtair Feko
=============== Optimisation variables ===============
No. Name Beg.value Minimum Maximum
1 sigma 3.503500000e+07 1.000000000e+07 5.000000000e+08
=============== Optimisation goals ===============
No. Name Expression
1 search1.goals.nearfieldgoal1 nearfieldgoal1 =============== Optimisation method: SIMPLEX NELDER-MEAD ===============
Maximum number of iterations: 1000
Base of the simplex: 1.500000000e-01
Reduction factor of the base: 5.000000000e-01
Termination at minimal base: 1.000000000e-03
Termination at standard deviation: 1.000000000e-04
Standard reflection coefficient (R): 1.000000000e+00
Contraction coefficient (-C, +C): 5.000000000e-01
Expansion coefficient (E): 2.000000000e+00
=============== SIMPLEX NELDER-MEAD: Intermediate results ===============
No. sigma nearfieldgoal1 global goal operation global best aim
1 3.503500000e+07 6.488107157e-02 3.488107157e-02 ----- 3.488107157e-02
2 3.774988237e+07 5.929294284e-02 2.929294284e-02 ----- 2.929294284e-02
3 4.516707895e+07 6.328463622e-02 3.328463622e-02 -----
4 4.788196133e+07 5.795280540e-02 2.795280540e-02 R 2.795280540e-02
5 5.430544199e+07 5.500882669e-02 2.500882669e-02 E success 2.500882669e-02
6 4.153550651e+08 3.036429062e-02 3.642906239e-04 R 3.642906239e-04
7 4.356175335e+08 2.964433899e-02 3.556610122e-04 E success 3.556610122e-04
8 4.457496125e+08 2.929870383e-02 7.012961666e-04 R
9 4.356179559e+08 2.964446921e-02 3.555307926e-04 +C success 3.555307926e-04=============== SIMPLEX NELDER-MEAD: Finished ===============
Optimisation finished (Standard deviation small enough: 5.020322005e-06)
Optimum found for these parameters:
sigma = 4.356179559e+08
Optimum aim function value (at no. 9): 3.555307926e-04
No. of the last analysis: 9
Sensitivity of optimum value with respect to each optimisation parameter,
i.e. the gradient of the aim function at 1% variation from the optimum:
Parameter Sensitivity
sigma 8.344260771e-01