実際のケース: ボリューム導体
概要
ここでは、(断面領域を無視できない)2つのボリュームの並列導体の実際のケースにおける、部分インダクタンスの解析式を示します。この式は、各導体の幅と厚みでの連続積分により、前の式から推測されます。
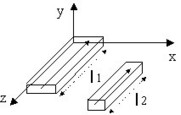
留意事項:セグメントS1とS2の間の部分インダクタンスは、次の式で表されます:
![]()
計算の仮定
計算での仮定を以下に示します:
- 導体の断面領域での電流密度は均一です。
- 導体の断面は長方形の形状です。
式の取得
ボリューム導体間の部分インダクタンスの最終式は、次の図に示す4つの連続積分の後に得られます。
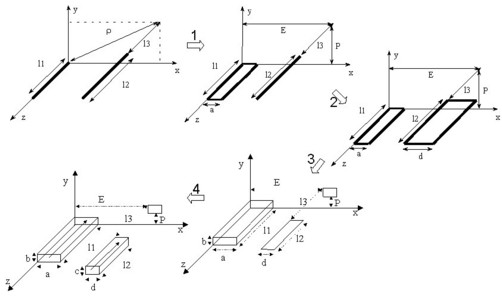
2つの導体の形状設定に従って、たとえばこの2つが非常に離れている場合は、あまり複雑でない式を得るため、さまざまなレベルで積分を停止することができます(幅全体の積分、厚みでの積分など)。
2つの導体間の部分インダクタンス
以下に示す構成での2つの導体間の部分インダクタンスのスタディについてはさらに検討が行われています。
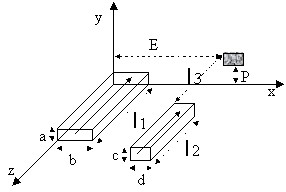
次の解析式により、µH単位での相互インダクタンスの値が得られます(距離の単位がcmの場合)。
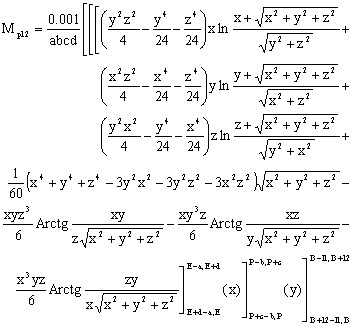
ここで:
![]()
導体の部分インダクタンス
ボリューム導体の部分インダクタンスは特殊ケースです。これは、前の式に、a = c、b = d、l1 = l2、l3 = 0、E = 0、P = 0を当てはめることで得られます。