回転機械のコンポーネント：かご形（2D）

かご形

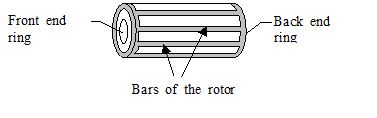
非同期機械のかご形は、2つのエンドリングを金属バーでつなぎ、円筒状にしたアセンブリです（次の図をご参照ください）。

かご形コンポーネントは、機械のかご形の電気回路を表現するマクロコンポーネント（サブ回路）です。

用途

このコンポーネントはTransientアプリケーションで使用でき、運動学的連成を使用する必要があります。

かご形：電気回路コンポーネント

かご形の電気回路には次のコンポーネントがあります：

各回転子バーのソリッド導体
エンドリングをシミュレートするために各導体に設けた両端間の抵抗器とコイル

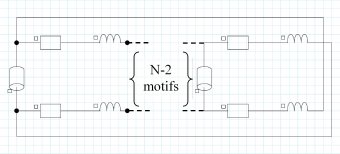
これらの情報を次の図に示します。

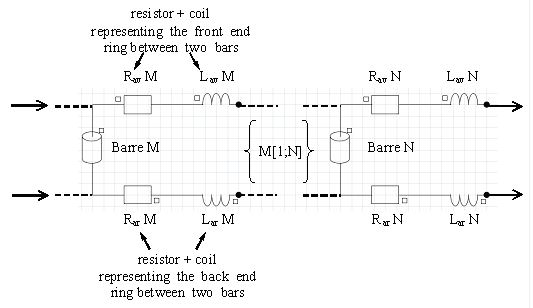
かご形のバーの本数をNとすると、この電気回路にはN個のソリッド導体、2N個の抵抗器、2N個のコイルがあります。

かご形： 2種類の電気回路クローズ方法

機械の表現モードを機械の部分的モデル化（1/4や1/2など）または機械全体のモデル化のどちらにするかに応じて、かご形の電気回路には2種類のクローズ方法があります。

したがって、電気回路のクローズ方法は、その回路に対応する有限要素ドメインの境界に割り当てた境界条件と関連付けられています。

周期的クローズ：モーター全体を記述している場合、または目的の部品が、それに隣接する部品に対して物理的に対称である場合（有限要素ドメインに偶数個の極が表現されている場合）。
非周期的クローズ：記述しているモーター部品が、それに隣接する部品に対して物理的に非対称である場合（有限要素ドメインに奇数個の極が表現されている場合）。

この2種類の電気回路クローズ方法を次の図に示します。

周期的クローズ：モーター全体、対称性（偶数極数）

=

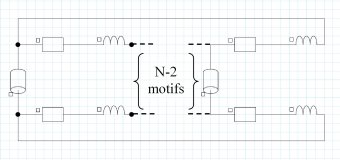非周期的クローズ：非対称性（奇数極数）

=

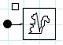
かご形マクロコンポーネントの特性

かご形マクロコンポーネントは次の4つのパラメータで定義します：

モデル化したモーター部分（有限要素ドメイン）に存在するバーの本数N
隣接する2本のバーの間に相当するエンドリング部の抵抗値R
隣接する2本のバーの間に相当するエンドリング部のインダクタンスL