磁気機械連成： 解析の基本

磁気機械連成

磁気機械連成では、問題の磁気的特性と運動学的特性が考慮されます。磁気的特性はマクスウェルの方程式で記述し、運動学的特性は並進運動と回転運動における基本的な動力学方程式で記述します。

電磁気学の各種方程式

この計算に使用する方程式を以下に示します：

• 電磁気学のマクスウェルの方程式： 、、
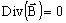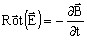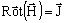
• その他の方程式： 、、

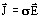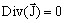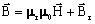
並進運動における基本的な動力学方程式

並進運動しているボディの動力学は、次の基本的な方程式で表現します。

$m\frac{{\partial }^{2}y}{\partial t^2}=\mathrm{\Sigma }{\overrightarrow{F}}_{ext} \Rightarrow m\ddot{y}=F_{em}-F_r$

ここで：

• m： 移動ボディの質量
• y： ボディの瞬時位置、ÿ： ボディの線加速度
• F_r： ボディに作用する機械的抵抗力
• F_em： ボディに作用する電磁力

回転運動における基本的な動力学方程式

ボディの回転運動に関する動力学方程式は次のとおりです。

$J\frac{{\partial }^2\theta }{\partial t^2}=\mathrm{\Sigma }{\overrightarrow{\mathrm{\Gamma }}}_{ext} \Rightarrow J\ddot{\theta }={\mathrm{\Gamma }}_{em}-{\mathrm{\Gamma }}_r$

ここで：

• J： 回転ボディの慣性モーメント
• θ： ボディの角度位置、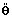： ボディの角加速度
• Γ_r： ボディに作用する機械的抵抗トルク
• Γ_em： ボディに作用する電磁トルク

解析の基本

磁気機械連成は、問題の電磁的特性と運動学的特性との弱い連成です。この問題を解析するには、次の表に示す4段階の手順を適用します。各時間ステップで、電磁的特性を先に解析し、つづいて運動学的特性を解析します。

この手法のアルゴリズムを次の表に示します。

追加の註

移動パートに作用する電磁力と電磁トルクは仮想仕事法によって計算します。

移動パートに作用する機械力または機械トルクは問題の入力データなので、ユーザーが入力します。