2Dの例： ラプラスの電磁力の計算

概要

本項では、2Dでのラプラスの力の平均成分と変動成分の計算を示します。

定義： 留意事項

ラプラスの電磁力は、磁界に置いた導体に作用する力です。

数式

導体に作用する力は、ラプラスの法則を使用して次のように計算できます。

ここで：

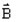• は導体が置かれた磁界の磁束密度
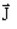• は導体内部の電流密度

ラプラスの力の平均成分と変動成分の式

ある時点の磁束密度と電流密度は次のようになります。

• 磁束密度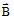は、と記述できます。

これは、楕円のパラメトリック方程式です（次の図をご参照ください）。

• 電流密度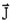は、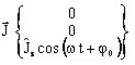と記述できます。

これらから、ある時点におけるラプラスの力の式は次のようになります。

ラプラスの力の平均成分と変動成分の式（続き）

したがって、ラプラスの力は以下の成分で構成されます：

• 平均成分：

  

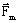
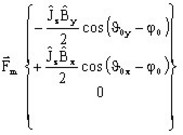
• 変動成分：

  

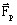
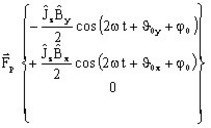
楕円による表現

この力は、空間的に下の図のように表現できます。

• 平均成分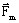は次の要素で定義できます：
  • 絶対値と、Ox軸を基準とした方向（角度α）

• 変動成分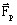は、角周波数2ωの楕円で記述できます。
  • 長軸： a
  • 短軸： b
  • Oxを基準とした長軸の方向（角度β）