スカラー量、フェーザーの概念

概要

ポスト処理に使用できる量は、スカラー量またはベクトル量です。

本項では、スカラー量を取り上げて、回転ベクトル、複素画像、フェーザーなどのいくつかの定義をもう一度確認します。

回転ベクトル、複素画像

脈動ωの経時変化する正弦スカラー量は、角速度ωで回転するベクトルによって幾何学的に表現できます。

このベクトルは、複素数の形状表現です。

例： 正弦波電流と複素画像

振幅が、脈動がω（ω = 2 π f）、t = 0における位相がβである経時変化する正弦波電流i(t)があるとします。

この電流iの瞬時値i：i = Î.sin(ω.t + β)

は、次の複素数iの虚部に等しくなります：i = Im(i)

速度ωの回転ベクトル	周期T=2 π/ωの正弦量i(t)

正弦波電流の複素瞬時値は、次の関係によって求められます：

• 直交形式： i = Î.cos(ω.t + β) + j.Î.sin(ω.t+ β)
• 指数関数形式： i = Î.e j(ω.t+ β)

ここで：

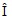• は複素数値iの絶対値
• ωt + βは複素数値iの偏角（または位相）
• βは初期位相

回転ベクトルの複素表示

正弦量に割り当てられた回転ベクトルは、複素数Aの形式で表されます。この複素数は次のように記述できます：

• 直交形式：
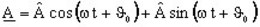
• 指数関数形式：

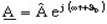
フェーザーの概念

正弦量A(t)に関連付けられた複素関数は、次のように2つの因数に分解できます：

この分解を次の表に示します。

因数	記述	説明
		t = 0における量A(t)に関連付けられた回転ベクトル
		角度ωtのベクトル回転

• 因数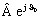には、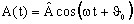という量の振幅と初期位相に関する情報が含まれます。
• 因数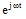には、この量の時間変動に関する情報が含まれます。

フェーザーの概念

時間ドメイン内の正弦関数は、フェーザーによって複素ドメイン内で表すことができます。

フェーザー： 定義

を、という量に割り当てられたフェーザーと呼びます。すなわち、という量に関連付けられたフェーザーは、t=0の時点におけるこの量に関連付けられた回転ベクトルです。