3Dの例:ドアミラーモーターの解析(技術文書)
前書き
このパラグラフは、技術文書:“ドアミラーモーターの解析でスタディされているケースの要約です。
このスタディ対象ケースに関連するファイルには、supervisorを介してアクセスできます。
実行するスタディ
技術文書“ドアミラーモーターの解析”で提示されているスタディでは、車のドアミラーを調整するために使用する直流モーターを取り上げています。
調査対象デバイス
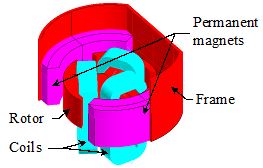
- 1つのフレームと2つの永久磁石で構成する固定パート
- 三角形状に配置して接続したコイルを持つ1つの3極回転子で構成する可動パート
動作原理
この簡潔な直流電気モーターの動作は以下のとおりです:
- コイルに電力を供給すると、電機子の周囲に磁界が発生します。電機子の左側が左の磁石による反発を受けて右の磁石に引き寄せられることで、電機子が回転し始めます。
- この原理で電機子が回転し続けます。
- 電機子が水平位置になると、コイルを流れる電流の方向が整流子によって反転し、磁界も反転します。以降はこのプロセスが繰り返されます。
スタディ対象ケース
次の5つのケースを実行します:
- ケース1とケース2: マルチスタティック運動モデルを使用したスタディ
- ケース3: 適用速度運動モデルを使用した過渡スタディ
- ケース4: 連成荷重運動モデルを使用した過渡スタディ
- ケース5: 巻線端インダクタンスを計算するパラメトリックスタディ
ケース1
1番目のケースは、マルチスタティック運動モデル(Magneto Staticアプリケーション)を使用したスタディです。
このスタディでは、回転子がさまざまな静的位置を取ります。フレームと回転子の材料は、比透磁率が一定(B(H)特性が線形)のステンレス鋼です。
回転子をさまざまな角度位置に置いて、永久磁石が生成する磁界に起因するコギングトルクを計算します。
ケース2
2番目のケースは、マルチスタティック運動モデル(Magneto Staticアプリケーション)を使用したスタディです。
このスタディでは、回転子がさまざまな静的位置を取ります。フレームと回転子の材料は、B(H)特性が非線形なステンレス鋼です。
回転子をさまざまな角度位置に置いて、永久磁石が生成する磁界に起因するコギングトルクを計算します。
ケース3
3番目のケースは、適用速度運動モデル(Transient Magneticアプリケーション)を使用したスタディです。
このスタディでは、回転子が一定の速度で回転します。フレームと回転子の材料は、比透磁率が一定(B(H)特性が線形)のステンレス鋼です。3つのコイルには電圧源から電源を供給します。
4,000rpmの既知の回転速度における電磁トルクとコイル電流を計算します。
ケース4
4番目のケースは、連成荷重運動モデル(Transient Magneticアプリケーション)を使用したスタディです。
このスタディでは、外部負荷がない状態でモーターの回転を開始します。フレームと回転子の材料は、B(H)特性が非線形なステンレス鋼です。3つのコイルには電圧源から電源を供給します。
モーターの回転が始まるときの回転子の角速度を計算します。
ケース5
5番目のケースは、巻線端インダクタンスを計算するパラメトリックスタディです(Magneto Staticアプリケーション)。
このスタディでは、回転子の高さがさまざまな値を取ります。フレームと回転子の材料は、B(H)特性が線形(比透磁率が一定)のステンレス鋼です。コイルには定電流源から電源を供給します。
回転子がさまざまな高さを取ったときの磁束を計算します。