結果の説明：磁束とインダクタンス（理論値）

磁束： 定義

磁界に配置されたサーフェスSについて考えます。このサーフェスSを貫く磁束密度の流束は次のように表されます：

ランダムなサーフェスを貫く磁束

磁束に対して垂直なサーフェスで、このサーフェスでの磁束密度が均一な場合、結果は次のようになります：

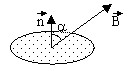
磁束密度を基準にして、法線がランダムな方向を向いているサーフェスについては、基本磁束は次のとおりです：

したがって、ランダムなサーフェスを貫く磁束は、そのサーフェスの積分となります：

3Dでは、異なる磁気スカラーポテンシャルによってモデル化された2つの領域とサーフェスが接触している場合、そのサーフェスの各面の結果は異なる可能性があります。このことは、スカラーポテンシャルによるモデル化では、磁束密度の法線成分B_nの連続性は確実には保証されませんが、磁界強度の接線成分H_tの連続性は保証されるという事実によって説明されます（これとは対照的に、ベクトルモデルでは、B_nの局所連続性は保証されますが、H_tの局所連続性は保証されません）。

コイル内の磁束

N回巻きのコイルの場合、そのコイルを貫く磁束は次の式によって表されます：

ここで：

は、1巻きで“認識”される磁束

は、N巻きで“認識”されるコイル内の合計磁束

コイル内の磁束を計算するには、そのコイル形状にほぼ対応しているサーフェスを貫く磁束を計算します。この方法は正確ではありませんが、十分有効になり得ます（特に相互磁束計算の場合）。他の磁束計算方法を以下に示します。

コイルの自己インダクタンス

電流I_kが流れ、貫く磁束の合計がΦ_kのコイルkの自己インダクタンスは、次の関係で与えられます：

この関係は、線形問題については次のように記述できます：

2つのコイル間の相互インダクタンス

2つのコイル（jとk）間の相互インダクタンスは、次の関係によって与えられます：

この関係は、線形問題については次のように記述できます：

ここで：

• Φ_jは、コイルj（無通電）内の磁束
• I_kは、コイルk内の電流