結果の説明: Fluxで実行される磁束の計算
留意事項: FE / 回路のリンク
有限要素ドメインと電気回路の間のリンクに関する留意事項を以下に示します:
| 回路 | 有限要素 |
|---|---|
| 電気回路に存在するもの | 有限要素ドメインに存在するもの |
| コイル導体タイプのコンポーネント |
コイル導体タイプの領域 または 非メッシュ化コイル(3Dのみ) |
| ソリッド導体タイプのコンポーネント | ソリッド導体タイプの領域 |
磁束計算の可否
次の表に、次元と方法に応じて使用できる磁束計算を示します。
| 2D平面 | 2D軸 | 3D | ||
|---|---|---|---|---|
| 回路 | コイル導体タイプのコンポーネントについての計算 | |||
| ソリッド導体タイプのコンポーネントについての計算 | ||||
| 有限要素 | 領域についての計算 | |||
領域についての計算
領域での磁束計算のためにFluxソフトウェアで使用される式は次のとおりです:
磁束: ![]()
ここで、![]()
J: 電流密度
i: 1巻きでの電流
φ: 1巻きを貫く磁束
A: ベクトルポテンシャル
S: 領域面積
V: 領域体積
n: 巻き数
2Dのコイル導体についての計算
2Dのコイル導体での磁束計算は、前述した領域での計算で使用される式と同じです。
この式は、コイル導体が割り当てられたすべての領域に適用されます。
3Dのコイル導体についての計算
次の計算は、3Dのコイル導体での磁束計算にのみ適用できます。
コイル導体を使用して、以下によって«印加電流»または«連成回路»タイプのコイルをモデル化できます:
- コイル導体タイプの領域
- 非メッシュ化コイル
コイルk内の流束Φkは、このコイル内の電流Ikを基準にした磁気随伴エネルギーWm'の導関数によって表されます:
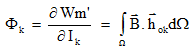
hok: 流れる電流が1Aの場合に真空内でコイルkによって生じる磁界
![]() : スタディドメイン
: スタディドメイン
このコマンドは、コイル導体タイプの電気コンポーネントに適用され、コイルに直接適用されることはありません。1つのコンポーネントにより複数のコイルを再グループ化できるためです(特に対称性や周期性のケースで)。
計算された磁束は、その電気コンポーネントに“属している”すべてのコイルの巻線のアセンブリを“貫く”合計磁束です。巻数は合計巻数です。すなわち、各コイルの巻数の合計です。
非メッシュ化コイルに関する3Dの特殊性:結果の精度はメッシュ、特にコイル周辺のメッシュに依存しています。磁束計算の精度を高めるためには、コイルを幾何学的に記述してメッシュ化することが有効である可能性があります。2次要素が使用されている場合は、精度が向上します。
インダクタンス: 自己 / 相互
線形モデルの場合は、磁束の計算後に、等価インダクタンスを推定できます。
複数のコイルに同時に電流が供給されている場合、計算されるインダクタンスは、全体インダクタンスLです。これには、選択したコイルL11の自己インダクタンスと、他の通電コイルM12、M13などに起因する相互インダクタンスが含まれます。
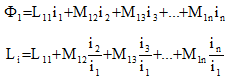
コイルの自己インダクタンスを計算するには、他のコイル内の電流はゼロである必要があります。このような状況では、この値は、システムの全体エネルギーWを計算して得ることもできます:
![]()
非通電コイル(I2=0、I3=0など)を貫く磁束によって、通電コイルとの相互インダクタンスを推定できます:
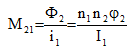
デバイスのインダクタンスのマトリックスを計算するには、各通電コイルの解が必要です。
インダクタンスの2Dモデル化ルール
コイルのモデル化は、使用されるケースに応じて異なります。コイルインダクタンスの推定は異なる可能性があります。
次の表に、使用されるモデル化に応じたコイルインダクタンスの計算に関する必要な情報を示します:
| インダクタンスの推定 | 補足 | ||
|---|---|---|---|
| 2D平面 | 対称性 / 周期性なし |
コイルの内側領域と外側領域が記述されている場合、このコイルのインダクタンスは、その内側領域と外側領域について計算されたインダクタンスの合計と同じです:
|
調査対象のデバイスが平衡状態になるように(電流源の積分がゼロになるように)、各コイルの内側領域と外側領域には同時に電流が供給されている必要があります。 |
| 対称性 / 周期性あり |
対称性または周期性により外側領域のみが記述されている場合、このコイルのインダクタンスは、外側領域について計算されたインダクタンスの2倍となります。
|
平面内の、無限ボックスなしの状態で、対称性によりコイルの外側部分のみが記述されている場合は、内側部分は境界条件によってシミュレートされる必要があります。この条件が適用されない場合、得られるインダクタンスの値は正しくない可能性があります。 | |
| 2D軸 |
領域について計算されるインダクタンスは、対応するコイルのインダクタンスです:
|
1つのコイルを記述するために必要な領域は1つのみであるため、1つの電流のみが供給されます。デバイスは自動的に平衡状態になります。 | |
Fluxと対称性 / 周期性
モデル化されたデバイスに対称性や周期性がある場合:
- コンポーネントについての計算では、Fluxは、対称性や周期性によって“元の”コイルとその“コピー”を考慮します。
この場合、Fluxでは以下が評価されます:
- 対称性や周期性の数とタイプを考慮する特定の係数
- コイルの関連付けタイプ(すべて直列またはすべて並列)を考慮するConductors in series or in parallelコマンド
- 領域についての計算では、Fluxは、表されたパートのみを考慮し、対称性や周期性は考慮しません。この場合、ユーザーは得られた結果に係数を適用する必要があります。
