Transient Magnetic: 解を求める方程式(ベクトルモデル2D)
概要
ベクトルモデルは、2Dアプリケーションの場合に提案される汎用モデルです。
ベクトルモデルを使用して解く方程式(2Dアプリケーション)
マクスウェル-ファラデー方程式![]() は、
は、![]() のように、電気スカラーポテンシャルVが存在することを意味します。
のように、電気スカラーポテンシャルVが存在することを意味します。
Transient Magneticアプリケーションで有限要素法によって解く方程式は次のように記述されます。
![]()
ここで:
- ν0は媒質の相対磁気抵抗率のテンソル
- ν0は真空の磁気抵抗率(ν0 = 1/µ0 = 1/(4π10-7))(m/H)
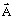 はベクトルポテンシャル(Wb/m)
はベクトルポテンシャル(Wb/m)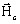 は保磁力(永久磁石)(A/m)
は保磁力(永久磁石)(A/m)
- σは媒質の導電率のテンソル(S)
- Vは電気スカラーポテンシャル(V)
状態変数、ベクトルモデル(2D)
状態変数は次のとおりです:
- 磁気ベクトルポテンシャル
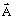
- 電気スカラーポテンシャルV
問題タイプ(平面2Dまたは軸対称2D)に応じた状態変数を次の表に示します。
| 問題のタイプ | 状態変数 |
Flux 3Dでの表記 |
|---|---|---|
| 平面 | An | AN1* |
| 軸対称 | rAn | RAN1* |