Steady State AC Magnetic: 解を求める方程式(概要)
概要
この解析で使用する方程式は次のとおりです:
- マクスウェルの方程式(磁気系の場合)
- 物質の構成方程式
Steady state AC Magneticアプリケーションの計算条件は次のとおりです:
- 状態変数は時間依存です: d/dt ≠ 0(定常状態正弦波: 電流源は時間とともに正弦関数で変化)
-
計算では、B、H、およびEの各界のみが考慮されます(D界は計算されません)。
電界のEとDの方程式と磁界のBとHの方程式は非連成化できません。
方程式と条件
ここで定義した計算条件の下では、各方程式は次のようになります:
|
E: 電界強度(V/m) B: 磁束密度(T) H: 磁界強度(A/m) J: 電流密度(A/m2) |
|||
|
σ: 導電率(S) µ: 透磁率(H/m) |
|||
磁性材料で主要な方程式は、次のように、B(H)またはH(B)の形式で表現できます。
| ⇒ |
µr: 比透磁率 µ0: 真空の透磁率 |
| ⇒ |
νr: 磁気抵抗率νr =1/µr ν0: 真空の磁気抵抗率ν0 =1/µ0 |
モデル
これらの方程式を解くために、次の2つのモデルを使用します:
-
磁気ベクトルポテンシャルを使用するベクトルモデル(表記は
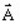 )
) -
磁気スカラーポテンシャルを使用するスカラーモデル(表記はϕtotまたはϕred)
モデルと2Dアプリケーションまたは3Dアプリケーション
2つのモデル(ベクトルとスカラー)が提案されます:- 2Dアプリケーション用のベクトルモデル
- 3Dアプリケーション用のスカラーモデル