Magneto Static： 解を求める方程式（スカラーモデル）

概要

スカラーモデルは、3Dアプリケーションの場合に提案される汎用モデルです。

このモデルは、3Dアプリケーションを解析するためにFlux 3Dの3Dソルバーによってデフォルトで（自動的に）使用されます。

スカラーモデルで解く方程式（3D）

方程式 を使用すると、 などのさまざまな磁気スカラーポテンシャルϕを導入できます。 項は磁界 （）の非回転部分ですが、 項は回転部分またはnullにすることができます。

はさまざまな方法で選択でき、 の選択によってスカラーポテンシャルが異なります。Flux 3Dには、さまざまなスカラーポテンシャルを使用するさまざまな磁気定式化があります。1つの定式化が問題の各領域に関連付けられているので、方程式も問題の各領域に関連付けられています。

静磁界アプリケーションでは、有限要素法によってスカラーモデルで解く方程式は一般的に次の形式で記述します。

ここで：

  • [µr]は媒質の比透磁率のテンソル
  • µ0は真空の透磁率で、µ0 = 4π10-7（H/m）
  • ϕは磁気スカラーポテンシャル（A）であり、ϕtotとϕredで表記する2つのポテンシャルがあります

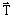  • は磁界源に対応する項

    （磁界源または電気ベクトルポテンシャル（A/m））

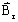  • は残留磁束（永久磁石）（T）

提示される定式化

スカラーモデルで提示される3つの定式化は、構成面からそれぞれ次の3つの状況に対応します：

この3つの状況で解を求める方程式を次に示します。

これらの定式化をそれぞれ別々に使用すると著しい制限が発生しますが、結合して使用すると効率的な汎用モデルが形成されます。

全スカラーポテンシャル（3D）

電流源が存在しない場合は、全磁気スカラーポテンシャルϕtotを使用します。電流密度 は0です。このケースは、スカラーモデルの一般方程式で とした状況に相当します。

磁界強度 は で記述され、

解を求める方程式は になります。

状態変数は、全磁気スカラーポテンシャルϕtotです。

Fluxでは、この変数はV1と記述されます。

Hjを基準とする縮小磁気スカラーポテンシャル（3D）

電流源が非メッシュ化タイプの場合は、Hjを基準とする縮小磁気スカラーポテンシャルϕredHjを使用します。このケースは、ビオ・サバールの公式でHjを解析的に計算したスカラーモデルの一般方程式で とした状況に相当します（§Magneto Static： 非メッシュ化供給源（3D固有）をご参照ください）。

磁界強度 は で記述し、

解を求める方程式は になります。

状態変数は、Hj:を基準とする全磁気スカラーポテンシャルϕredHjです。

この変数はFluxではV1Rと記述されます。

T0を基準とする縮小スカラーポテンシャル（3D）

電流源がメッシュ化タイプの場合は、T0を基準とする縮小磁気スカラーポテンシャルϕredToを使用します。このケースは、スカラーモデルの一般方程式で とした状況に相当します。量 は の関係を満足します。 は、磁力源のメッシュ化領域における電流密度です。

磁界強度 は で記述し、

解を求める方程式は になります。

したがって、状態変数は次のようになります：

  • T0を基準とする縮小磁気スカラーポテンシャルϕredTo

    この変数もFluxではV1Rと記述されます。

  • 電気ベクトルポテンシャル 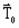。Fluxでは直接アクセスできない変数です。