等方性 / 異方性材料

概要

スタディの対象とする材料は等方性でも異方性でもかまいません。つまり、材料の磁気的挙動は次のいずれかになります：

  • 適用した磁界の方向に依存しない挙動（等方性材料）
  • 適用した磁界の方向に依存する挙動（異方性材料）

以降の各項では、この2つのケースを取り上げます。

等方性材料

等方性材料の特徴は、その磁化法則が、適用した磁界の方向に依存しない点にあります。

ベクトルと ベクトルは必ず同一線上にあります。

と との依存性は、B = µHと記述できるスカラー関係です。

註：

  • 線形近似の場合：

    µは定数なのでB = µHと記述できます。

  • 非線形近似の場合：

    µはHに依存する値なのでB =µ(H).Hと記述することが適切です。

異方性材料

異方性材料の特徴は、その磁化法則が、適用した磁界の方向に依存する点にあります。

ベクトルと ベクトルは同一線上にありません。

と との依存性は、 と記述できるベクトル関係です。

µは透磁率のテンソルで、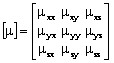 となります。

註：

  • 線形近似の場合：

    µijは定数なので 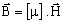と記述できます。

  • 非線形近似の場合：

    µijはHに依存する値なので 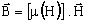と記述することが適切です。

異方性に関する注意

異方性のタイプは次のいずれかです：

  • 材料の結晶構造に関連する結晶異方性
  • 磁心の積層構造に関連する異方性（“偽異方性”）。この異方性の形態は、«磁性非導電性積層領域»と呼ばれる特定の領域を通して考慮されます（物理特性：基本の章をご参照ください）。

結晶異方性（平面での異方性）

結晶異方性を考慮できるようにするモデルは、2D異方性（平面のみでの異方性）に重点を置いたモデルです。

このようなモデルでは、主に主方向、積層方向DL、および横断方向DTで、シートの数値化した磁気特性を扱います。

Nahil HIHATの論文から、以下のモデルを引用できます：

  • 軸分離のモデルNIYS75
  • 2つの軸のモデルHLN84
  • 楕円形モデルおよび軸回転が存在する楕円形モデルDNP83
  • 経験的異方性モデルなど

シートの優先方向：

  • DL： 積層方向
  • DT： 横断方向
  • DN： 法線方向

参考文献

異方性磁性材料のモデリングに関する補足情報については以下の文献をご参照ください：

  • “Quasi 3D Models for the Analysis of Structures Presenting a 3D Anisotropy”- Nabil HIHATの論文 – 2010Université Lille Nord de France – UArtois
  • “Anisotropic and nonlinear laws of magnetization: modelling and experimental validation” - Thierry PERAの論文 – 1994INPG ()
  • “Contribution to the bi-dimensional and three-dimensional modelling of anisotropy phenomena in 3-phase transformers” - Jean Marc DEDULLEの論文 – 1990INPG ()

半解析的2Dモデル（シートの平面）に関する参考文献：

  • NIYS75 T. Nakata, Y. Ishihara, K. Yamada et A. Sasano :

    Non-linear analysis of rotating flux in the t-joint of a three-phase, three-limbed transformer core.

    In proceedings of Soft Magnetic Materials 2 Conference, pages 57-62.1975.

  • HLN84 D. Huttenloher, H.W.Lorenzen et D. Nusheler :

    Investigation of the importance of the anisotropy of cold rolled electrical steel sheet.IEEE Transactions on Magnetics , 20(5):1968 -1970, 1984.

  • DNP83 A. Di Napoli et R. Paggi :

    A model of anisotropic grain-oriented steel.

    IEEE Transactions on Magnetics , 19(4):1557-1561, 1983.

磁気異方性のモデリングの課題

異方性材料の透磁率は、適用した磁界に応じて変化する成分で構成したテンソル量となります。

したがって、次の3つの曲線のグループとしてベクトル関係B(H)を記述します：

  • Bx(Hx, Hy, Hz)
  • By(Hx, Hy, Hz)
  • Bz(Hx, Hy, Hz)

このタイプの曲線を実験レベルで記述することはきわめて困難です。磁束密度の大きさと方向の両方を磁界強度Hの関数として同時に測定できる必要があるからです。

一般的には、磁界強度Hと磁束密度Bが平行になる方向でのみ測定します。

このような特性があることを前提として、このような測定値をソフトウェアに入力し、必要な補間をソフトウェアの数値計算で実行する必要があります。

こうしたさまざまな理由から、現状は次のようになっています：

  • 簡素化したモデルは存在しますが、そのモデルが有効な領域は限られています。
  • 非線形異方性モデルについては、まだ検討が必要です。

簡素化したモデル

一般的に、簡素化したモデルでは、材料の主軸方向で発生する現象を分離して扱うことを基本としています。

この手法では、モデル化する材料を基準とする3つの主方向のベクトル関係B(H)を表現し、その関係を最も良好に再現できる補間処理（線形補間や楕円補間など）を実行します。

軟質磁性材料や永久磁石などの材料分類ごとに異なる方法で検討する必要があります。

Fluxの場合： 線形モデル

線形モデルとしてFluxに用意されている簡素化したモデルは、線形補間による軸の分離を取り入れています。

と とのベクトル依存性は と記述でき、3つの曲線Bx(Hx)、By(Hy)、およびBz(Hz)の形式で表現できます。該当の軸Ox、Oy、およびOzを磁化の主軸と呼びます。

透磁率のテンソルは 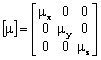となります。

解析の段階では、この純粋に数学的な形式がきわめて簡潔で扱いも容易です。この形式は、磁束密度と磁界強度が3つの主方向（優先方向、横断方向、および第3の方向）と微視的には同一方向にあるという事実を表しています。

異方性積層では、シート積層の方向、横断方向（シートの平面内）、およびシートに垂直な法線方向がこれらの3方向になります。

永久磁石では、磁化方向およびそれと直交する2つの方向がこれらの3方向です。

参考文献

異方性磁性材料のモデリングに関する補足情報については以下の文献をご参照ください：

  • “Lois d'aimantation anisotropes et non linéaires : modélisation et validation expérimentale”Thierry PERAの論文 – 1994INPG (Anisotropic and nonlinear laws of magnetization: modeling and experimental validation)
  • “Contribution à la modélisation bidimensionnelle et tridimensionnelle des phénomènes d'anisotropie dans les transformateurs triphasés” - Jean Marc DEDULLEの論文 – 1990INPG (Contribution to the bi-dimensional and three-dimensional modeling of anisotropy phenomena in 3-phase transformers)

Fluxの場合： 非線形モデル

線形異方性材料を考慮するためにFluxに用意されているモデルを非線形のケースに一般化することはできません。

そのことから、2Dの非線形材料向けに楕円補間による新しいモデルが作成されています。このモデルについて本書では詳しく説明しません。詳細については以下の文献をご参照ください。

Biroet al., 2010 Biro, O., Außerhoger, S., Preis, K., and Chen, Y. (2010).A modified elliptic model of anisotropy in nonlinear magnetic materials.COMPEL：The Internationnal Journal for Computation and Mathematics in Electrical and Electronic Engineering , 29(6):1482 – 1492.

Dedulle et al., 1990 Dedulle, J.-M., Meunier, G., Foggia, A., Sabonnadiere, J.-C., and Shen, D. (1990).Magnetic fields in nonlinear anisotropic grain-oriented iron-sheet.IEEE Transactions on Magnetics , 36(2):524 – 527.

Napoli and Paggi, 1983 Napoli, A. D. and Paggi, R. (1983).A model of anisotropic grain-oriented steel.IEEE Transactions on Magnetics , 19(4):1557 – 1561.