Analysis Entities
Nine types of modeling element containers are used to define the analysis. One sub-system (a drive torque controller) is also included in the analysis.
Thirteen modeling element types are used in the front analysis and fourteen modeling element types are used in the rear suspension analysis (see below). The sub systems “Jack” and “Marker for Request” are also described below.
Attachments
The analysis uses the standard analysis attachment. The attachments resolve automatically if the model is built through the Model Wizard. The attachments contain the minimum data the analysis needs to run the analysis. The attachments are standard for most analyses.
Bodies
Two bodies are used in the Front Half Static Ride analysis, Jack and Dummy body. The Jack is used to simulate a platform moving vertically to displace the suspension. The Dummy body is included in the analysis to make the system compatible with ADAMS modeling. The Dummy body is attached to the knuckle with a fixed joint and has no role in the analysis when it is run in MotionSolve.
In a Rear suspension analysis, the Dummy body for DOF body is included to make the degrees of freedom work out for certain suspensions. The Dummy body is constrained to ground with a soft bushing.
Bushings
There are no bushings in the Front Suspension analysis. One bushing is included in the Rear Half Suspension analysis, “Dummy bush for DOF”. The Dummy bush for DOF constrains the Dummy Body for DOF body to ground with a soft bushing rate. The bushing is used to make the Degrees of Freedom work properly for certain models.
Datasets
Two datasets are used in the system, Vehicle Parameters and Suspension travel. The Suspension travel dataset is used to store the suspension travel inputs for jounce and rebound. Edit the parameters on the Suspension travel form. The Vehicle Parameters dataset is used to store data used to calculate the Suspension Design Factors. Edit the input values on the Vehicle Parameters form. The input values, and their use is described in depth in the Suspension Design Factors section.
Forces
The Front and Rear Static Ride analyses include one force pair, the Jack Vertical Actuator. This force applies a vertical force on the jack which moves the suspension into jounce and rebound. The force is controlled by a DIF statement.
Forms
Two forms are included in the Static Ride analysis. These forms are used to modify the inputs into the analysis. The Vehicle Parameters form is used to edit the inputs used to calculate the Suspension Design Factors. The Static Ride Parameters are the jounce and rebound travels used in the analysis. Modify the values to match the desired wheel center vertical travel in your suspension. The front and rear forms are the same.
Graphics

Figure 1. Jack Graphics Example
Joints
Two joints, “dummy fixed to knuckle” and “rack dummy ball” joints are included in the Front Half Static Ride analysis; the dummy fixed to knuckle joint is also. included in the Rear Half Static Ride analysis. Dummy fixed to knuckle is a fixed joint which attaches the knuckle to the dummy body. The dummy joints are included to constrain dummy bodies. The dummy bodies are used to make certain analyses work with ADAMS.
Markers
| Marker Label | Marker Varname | Description | Use |
|---|---|---|---|
| Wheel Center | mrk_wc | Marker pair on the dummy body at the wheel center, Z axis pointing inboard, ZX plane of the marker along global X. | The primary wheel center marker pair, used in the system that actuates the suspension motion and used to calculate the SDFs in the SDF subroutine. |
| WC marker at Ground | mrk_gnd | Marker pair on ground at the wheel center; Z axis along global Z and ZX plane along global X. | Used in the system that actuates the suspension motion and used to calculate SDFs in the SDF subroutine. |
| Kingpin Axis Marker | mrk_kp | Marker pair on the knuckle, at the LBJ or estimated LBJ location, with a Z axis pointing at the actual or estimated UBJ location. | Used to calculate the vehicle kingpin metrics in both a user output request and in the SDF subroutine. The marker Z axis is used for the calculations. |
| Wheel Patch Marker | mrk_patch | Marker pair on the wheel at the tire patch location. The tire patch location is calculated using the SLR entered on the Vehicle Parameters form, and is the “Jack GeomU” point. The marker Z axis is along global Z and the marker X axis is in the global ZX plane. | Used to calculate the roll angle/track width in the user defined expression output. |
| Ground Patch Marker | mrk_patch_grnd | Marker pair on body “ground” at the tire patch location. The tire patch location is calculated using the SLR entered on the Vehicle Parameters form, and is the “Jack GeomU” point. The marker Z axis is along the global Y (lateral) axis and the marker X axis is in the global X plane. | Not currently used in the MotionSolve analysis. |
| Marker Label | Marker Varname | Description | Use |
|---|---|---|---|
| Wheel Center Marker | mrk_wc | Marker pair on the dummy body at the wheel center, Z axis pointing inboard, ZX plane of the marker along global X. | The primary wheel center marker pair, used in the system that actuates the suspension motion and used to calculate the SDFs in the SDF subroutine. |
| WC marker at Ground | mrk_gnd | Marker pair on ground at the wheel center; Z axis along global Z and ZX plane along global X. | Used in the system that actuates the suspension motion and used to calculate SDFs in the SDF subroutine |
| Ground Reference at Contact Patch | Tcp_grnd | Marker pair on body ground at the Jack Geomu point (tire patch). The marker Z axis is along the global Z and the XZ plane of the marker is along the global X axis. | This marker is not used in the MotionSolve analysis. |
| Ground Reference at wc | wc_grnd | Marker pair on ground at the wheel center location. The marker Z axis is along global Z and the marker X axis is in the global ZX plane. | This marker is not used in the current MotionSolve analysis. |
| Kingpin Axis Marker | mrk_kp | Marker pair on the knuckle, at the lower ball joint or estimated lower ball joint location, with a Z axis pointing at the actual or estimated upper ball joint location. In strut type suspensions the marker Z axis points at the top of the strut. | Used to calculate the vehicle kingpin metrics in both a user output request and in the SDF subroutine. The marker Z axis is used for the calculations. |
| Wheel Patch Marker | mrk_patch | Marker pair on body ground at the Jack geomu point (tire patch). The marker Z axis is along the global Z (lateral) axis and the marker ZX plane axis is in the global X plane. | Not currently used in the MotionSolve analysis. |
Motions
Two motions are included in the Front Half Static Ride analysis, and a single motion is included in the Rear Half Static Ride analysis. The wheel spindle motion is used in both front and rear, and the steering wheel motion is used in front analysis. The wheel spindle motion fixes the wheel to the knuckle to prevent wheel rotation. The steering wheel motion is used to hold the steering wheel during most analyses, and is used to turn the steering wheel during a steering analysis. The wheel spindle motion is deactivated and not used in both the Front and Rear Ride analyses.
Outputs
45 outputs are included in both Front and Rear Static Ride analyses.
Points
| Point | Description | Use |
|---|---|---|
| Jack GeomL (Jack Geometry Lower) |
A point 320 mm below the jack GeomU point. | Used to define the jack geometry. The 320 mm is an arbitrary number. |
| Jack Geomu (Jack Geometry Upper) |
An estimate of the tire patch location, calculated using the wheel center location, the spindle axis , and the SLR entered in the Vehicle Parameters form. | Used in SDF calculations and as the location to transfer load from the test rig platen to the wheel. |
Solver Arrays
| Vehicle Parameter Array | Description | Use |
|---|---|---|
| Ds_vehpar.veh_end.ival | Vehicle End: 1=front suspension; 2=rear suspension; 3=2nd rear suspension |
Communicates the suspension type to the SDF subroutine. The subroutine calculates different values for certain parameters depending on which end of the vehicle is being analyzed. |
| Ds_vehpar.dif_mnt.ival | Differential Mount type 0=mounted to body 1=Unsprung mount (integral with the axle) |
Used in the SDF calculations in the anti-lift and anti-dive calculations. |
| Ds_vehpar.tire_slr.value | Tire Static Loaded Radius in mm | Used to locate the Jack GeomU point and in many of the SDF calculations. |
| Ds_vehpar.tire_rate.value | Tire Spring Rate in N/mm | Used in the SDF calculations |
| Ds_vehpar.cg_height.value | Vehicle CG height, measured from ground to the CG in the Z direction (mm) | Used in the SDF calculations (especially the Anti-lift and anti-dive calculations) |
| Ds_vehpar.wheel_base.value | Vehicle Wheelbase (mm) | Used in the SDF calculations (especially the Anti-lift and anti-dive calculations) |
| Ds_vehpar.front_brake.value | The Ratio of front brake torque to total brake torque (typically .6 to .7). | Used in the SDF calculations (especially the anti-lift and anti-dive calculations) |
| Ds_vehpar.front_drive.value | The ratio of the engine torque applied to the front axle divided by total torque. | Used in the SDF calculations (especially the anti-lift and anti-dive calculations) |
| Ds_vehpar.axle_ratio | The nominal Axle ratio of the suspension being analyzed. Typically in the 2.7-5.0 range. | Used in the SDF calculations (especially the anti-lift and anti-dive calculations) |
| Ds_vehpar.veh_weight.value | Total vehicle mass in Kg | Used in SDF calculations and in the vehicle load analysis ev |
| Parameter Name | Description | Use |
|---|---|---|
| mrk_wc.l.id | Left wheel center marker ID-marker at the left wheel center; Z axis points inboard along the spindle axis; ZX marker plane is along global X; the resulting marker Y axis is down. | The primary point location for left suspension SDF calculations. Most geometric properties and most compliant SDF parameters are calculated using this point as input. |
| mrk_wc.r.id | Right wheel center marker ID-marker at the right wheel center; the marker Z axis points inboard along the spindle axis; the marker ZX plane is along global X; The resulting marker Y axis is up. | The primary point location for right suspension SDF calculations. Most geometric properties and most compliant SDF parameters are calculated using this point as input. |
| mrk_kp.l.id | Left kingpin axis marker ID- the marker placed at the left lower ball koint or a location that defines a point on the left kingpin axis. The Z axis of the marker points to the left upper ball joint or a point that defines a point on the kingpin axis. | Marker Z axis is used for caster and kingpin inclination calculations for the left side of the vehicle. |
| mrk_kp.r.id | Right kingpin axis marker ID- the marker placed at the right lower ball joint or a location that defines a point on the right kingpin axis. The Z axis of the marker points to the right upper ball joint or a point that defines a point on the kingpin axis. |
Marker Z axis is used for caster and kingpin Inclination calculations for the right side of the vehicle. |
| mrk_gnd.l.id | The ID of the left wheel center marker on body ground. The marker is on the ground body at the left wheel center location. The marker Z axis is parallel to the global Z axis and the marker X axis is parallel to the global X axis. | Marker is used for the left wheel displacement control system and left wheel center displacement calculations in the SDF routine. |
| mrk_gnd.r.id | The ID of the right wheel center marker on body ground. The marker is on the ground body at the right wheel center location. The marker Z axis is parallel to the global Z axis and the marker X axis is parallel to the global X axis. |
Marker is used for the right wheel displacement control system and right wheel center displacement calculations in the SDF routine. |
| sfo_jack_actuator.l.i.id | I marker ID of the left force between the jack and ground that is used to actuate the left wheel suspension motion. | Forces are used for the SDF subroutine calculations and the force reported by the SDF routine. The I and J marker IDs are required to recover the correct force. |
| sfo_jack_actualtor.r.i.id | J marker ID of the left force between the jack and ground that is used to actuate the left wheel suspension motion. | Forces are used for the SDF subroutine calculations and the force reported by the SDF routine. The I and J marker IDs are required to recover the correct force. |
| sfo_jack_actuator.j.i.id | I marker ID of the right force between the jack and ground that is used to actuate the left wheel suspension motion. | Forces are used for the SDF subroutine calculations and the force reported by the SDF routine. The I and J marker IDs are required to recover the correct force. |
| sfo_jack_actualtor.j.i.id | J marker ID of the right force between the jack and ground that is used to actuate the right wheel suspension motion. | Forces are used for the SDF subroutine calculations and the force reported by the SDF routine. The I and J marker IDs are required to recover the correct force. |
| b_str_dummy.cm.id | Steering dummy body center of mass ID number. The center of mass marker for the dummy body attached to the steering rack. | Not used by the current subroutine but kept in the software to maintain compatibility with ADAMS simulations. |
 Figure 2. |
 Figure 3. |
Solver Differential Equations
The Front and Rear Half Static Ride analyses include two solver differential equations, differential left jack and differential right jack. The solver differential equations are part of the control system used to move the suspension through the requested travel. They are similar for both the front and rear suspensions.
IF(mode-4:0,0,1)*IF(mode-7:1,0,0)*(VARVAL(31000200)-VARVAL(31000100))A break down of the equation is provided below:
IF(mode-4:0,0,1)- When mode (the solution type of the solver) is less than or equal to 4 the expression evaluates to zero. When mode is greater than 4, the expression evaluates to one.
IF(mode-7:1,0,0)- When mode (the solution type of the solver) is less than or equal to 7 the expression evaluates to one. When mode is 7 or greater, the expression evaluates to zero.
VARVAL(31000200)- The solver variable value that represents the commanded displacement of the left wheel center Z displacement.
VARVAL(31000100)- The solver variable value that represents the actual displacement of the left wheel center in the global Z direction from the design position.
IF(mode-4:0,0,1)*IF(mode-7:1,0,0)- This expression is one for modes 5 and 6, which are statics and quasi-statics. For all other modes this evaluates to zero. This effectively turns the solver differential equation off for solution sequences other than statics and quasi-statics.
VARVAL(31000200)-VARVAL(31000100))- The commanded displacement minus the actual displacement. If the suspension is following the commanded value this will be zero.
The solver differential equation maintains the wheel displacement due to the following property of solver differential equations: For static and quasi-static solutions, the derivative of the dynamic state is set to zero. This converts the Control_Diff to an algebraic equation for these two analyses. See the Control Diff topic in the MotionSolve Reference Guide for additional information.
Solver Variables
- Variable Name
- Description
- Left feedback variable
- Global Z displacement of the left wheel center marker, relative to the original location of the left wheel center, in the global coordinate system.
- Left command variable
- Requested Displacement of the left wheel center. From 0-5 seconds a half sin function with a magnitude equal to the jounce travel defined on the static ride parameters form. From 5-10 seconds a half sin function with a magnitude equal to the rebound travel defined on the static ride parameters form.
- Right feedback variable
- Global Z displacement of the right wheel center marker, relative to the original location of the right wheel center, in the global coordinate system.
- Right command variable
- Requested displacement of the right wheel center. From 0-5 seconds a half sin function with a magnitude equal to the jounce travel defined on the static ride parameters form. From 5-10 seconds a half sin function with a magnitude equal to the rebound travel defined on the static ride parameters form.
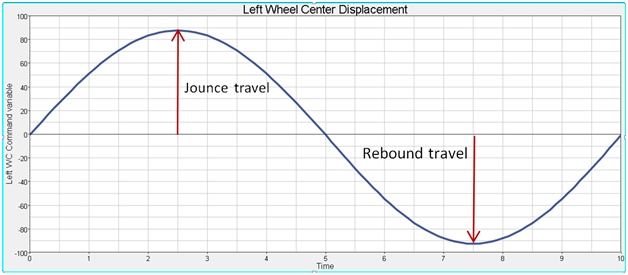
Figure 4.
Wheel Displacement Control System
Many of the half car analyses use a control system to displace the wheels in jounce and rebound. The system applies a force on the jack to move the wheel center through a displacement defined by the left command variable and right command variable. The control system only works while running statics and quasi-statics solutions.
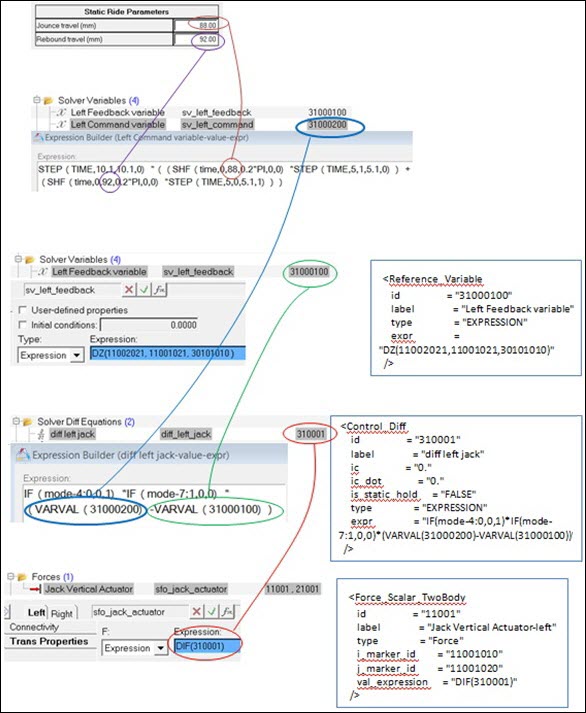
Figure 5.
- Jounce travel and rebound travel are entered in the Static Ride Parameters form. Travel is assumed to be symmetric.
- The solver variables left command variable (shown) and the right command variable (not shown) refer to the travels from the Static Ride Parameters form.
- The equations in the left command variable and right command variable create a sin wave which has a positive peak at 2.5 seconds with a magnitude equal to the jounce travel, and a negative minimum at 7.5 seconds at the rebound travel magnitude. The solver equation is further explained in the Solver Variables section below.
- The solver variables left feedback variable and right feedback variable are defined. The variable is the displacement of the wheel center on the wheel, relative to the original wheel center position, in the global Z direction.
- The solver differential equation is defined (for left and right side) to be the difference between the command variable and the actual variable. If the wheel center displacement follows the command variable, the differential equation will be zero. The eifferential equation is set to zero for solution e=sequences other than statics and quasi-statics using IF statements and the MODE variable.
- A force is defined that is equal to the control differential of the wheel.
- The solver differential equation maintains the wheel displacement due to the following property: “For static and quasi-static solutions, the derivative of the dynamic state is set to zero. This converts the Control_Diff to an algebraic equation for these two analyses.”
Form and Dataset Element
The wheel control system form is shown below. The Static Ride Parameters form contains the jounce and rebound travel that are applied to the suspension system. Travel is symmetric (L<->R). The jounce and rebound variables are defined in the suspension travel dataset. Dataset types and variable names are defined in the dataset; data is normally entered on the form.
Solver Variables
- Equation
- Description
- STEP(TIME,10,1,10.1,0)
- A step function that is one when Time is less than 10 and zero when time
is greater than 10.
This makes the entire equation evaluate to zero after T=10.
- SHF(time,0,88,0.2*PI,0,0)
- A simple harmonic function, Time based, Time offset of zero, magnitude of 88, Frequency=.2*pi, with zero phase shift and a zero average value.
- STEP(TIME,5,1,5.1,0)
- A step function that is one when time is less than 5 and 0 when time is
greater than 5.1.
This turns the jounce SHF off when T>5.1.
- SHF(TIME,0,92,0.2*pi,0,0)
- A simple harmonic function, Time based, time offset of zero, magnitude of 92, Frequency=.2*pi, with zero phase shift and a zero average value.
- STEP(TIME,5,0,5.1,1)
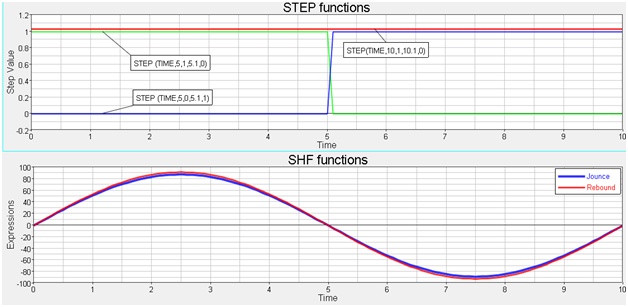
Figure 6. Step and SHF Functions in the Solver Variable Command Variable
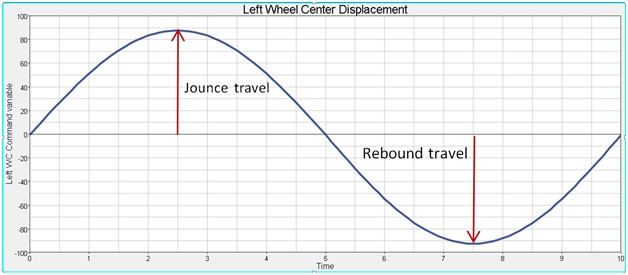
Figure 7. Resulting Left Command Variable vs Time
Solver Feedback Variable
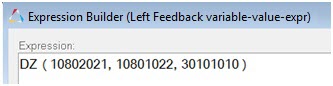
Figure 8.

Figure 9.
| Marker Number | Marker Symbol | Description |
|---|---|---|
| 10802021 | Mrk_wc.l.idstring | Marker on the wheel at the wheel center. |
| 10801022 | Mrk_gnd.l.idstring | A marker on ground at the wheel center. |
| 30101010 | MODEL.Global_Frame.idstring | A marker on ground at the global origin, with the same orientation as the global coordinate frame. |
Solver Differential Equations

Figure 10.

Figure 11.
Evaluated Expressions
The expression shown above uses the mode and if functions from MotionSolve, along with the VARVAL function. The combination of the two IF statements create logic that makes the DIF equal zero for all modes except statics and quasi-statics. The logic is shown in the truth table developed below:
| Mode | Mode Value | Mode-4 | IF(mode-4:0,0,1) | Mode-7 | IF(mode-7:1,0,0) | IF(mode-4:0,0,1) *IF(mode-7:1,0,0) |
|---|---|---|---|---|---|---|
| Kinematics | 1 | -3 | 0 | -6 | 1 | 0 |
| Reserved | 2 | -2 | 0 | -5 | 1 | 0 |
| Initial Conditions | 3 | -1 | 0 | -4 | 1 | 0 |
| Dynamics | 4 | 0 | 0 | -3 | 1 | 0 |
| Statics | 5 | 1 | 1 | -2 | 1 | 1 |
| Quasi Statics | 6 | 2 | 1 | -1 | 1 | 1 |
| Linear Analysis | 7 | 3 | 1 | 0 | 0 | 0 |
Actuator Force
The left and right side of the actuator force pair behave in the same manner. The force acts on the jack and is reacted on ground. The force acts in the vertical direction. The force is set to the DIF(308001) magnitude. When the DIF is evaluated during statics and quasi-statics, the derivative of the solver differential equation is set to zero. The result is that a force is generated by the DIF that forces the measured wheel displacement to follow the command wheel displacement.
- The prescribed wheel displacements for left and right wheel center Z displacement are defined by the expressions in the solver variables left command value and right command value.
- The force required to maintain the wheel displacement is defined by the force pair jack vertical actuator and is a pure Z force on the jack body on each side of the vehicle. This is set equal to the DIF value.
- The actual wheel displacements in the Z direction are defined by the solver variables left feedback variable and right feedback variable.
- The controls are defined in the diff left jack and diff right jack solver differential equations. They are the command solver variable minus the feedback solver variable. This will equal zero if the wheel is following the command input
- The solver treats the solver differential equation as an algebraic equation in statics and quasi-statics mode. As a result the DIF value is the force required to maintain the commanded wheel position.
Jack System
- Jack system joints
- There are two joint pairs in the jack system. The first joint is the “Jack Trans jt” which connects the jack body to ground with a translational joint at the lower end of the jack body. The joint is oriented in the Z (vertical) direction. The joint forces the jack to travel only in the vertical direction.
- Jack system vectors
- Three vectors are defined along the global X,Y, and Z axes, and are used to orient certain joints in the model.
Marker for the Request System

Figure 12. Left Wheel Center Marker