Imperfection
Imperfection is used in large displacement nonlinear static analysis, for example, to solve post-buckling problems combined with the arc-length method, among other techniques.
Usage
Geometric imperfection can be applied to stability sensitive structures which have difficulties in being solved, because of local or global buckling.
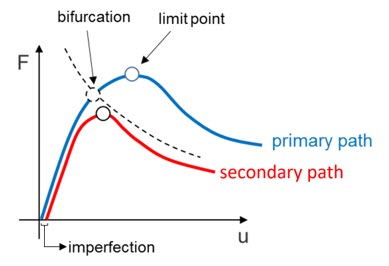
Figure 1. Stability Problem with Bifurcation Diagram
Interpretation
Theoretically, imperfection belongs to an operation in pre-processing of the finite element method. The original perfect mesh is changed to an imperfect one, by shifting the grid coordinates in translational directions. Applying an initial imperfection does not lead to any initial stresses and it is independent of the analysis type.
Strictly speaking, it is neither a boundary condition (Single Point Constraint or Enforced Displacement), nor an initial condition (initial velocity) in a transient sense. Further, the constrained grid or the degree of freedom can also contain certain imperfection.
Define Imperfection
- Use of the results in the form of H3D file
(TYPE=H3DRES) from an initial
analysis
The results of deformation or buckling modes (in case of a linear buckling analysis) from another analysis in the form of an H3D file is used with an amplitude/scaling factor to apply the initial imperfection. The H3D result file should exist already and should contain at least one subcase with displacement results or buckling modes.
- Apply the value of imperfection directly on the grid points
(TYPE=GRID)
Imperfection is defined directly on the GRID points based on the grid coordinate system in the IMPERF Bulk Data Entry.
The imperfection can be referenced to a certain subcase, from the OptiStruct input file (.fem), as outlined below.
Data Input
The ASSIGN card is used to specify a particular ID to the H3D result file (for TYPE = H3DRES):
ASSIGN, H3DRES, <assign_id>, <h3d_file>
IMPERF is used to assign the imperfection to a particular subcase.
Imperfection is supported in small/large displacement, static/transient analyses.
IMPERF Bulk Data Entry
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| IMPERF | ID | TYPE |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| H3DRESID | SUBID | NRES | FACT | GSET |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| G | X | Y | Z |
Multiple imperfection cards can be assigned to multiple Subcase Entries and each imperfection card could be referenced to multiple H3D files.
Input File Example
ASSIGN, H3DRES, 11, ./buckling_modes.h3d
SUBCASE 101
Analysis = NLSTAT
NLPARM(LGDISP) = 1
IMPERF = 2
….
BULK DATA
IMPERF, 1, H3DRES
11, 100, 1, 1.0 $$ H3D file with id 11, Subcase 100, mode 1, scaling factor 1.0
11, 100, 2, 0.5 $$ H3D file with id 11, Subcase 100, mode 2, scaling factor 0.5
11, 100, 3, 0.1 $$ H3D file with id 11, Subcase 100, mode 3, scaling factor 0.1Some examples of solving Post-buckling problems with imperfection are outlined below.
Example 1: Post-buckling of Euler Column
The post-buckling behavior of a classical Euler column subjected to a vertical loading of 106 N at the top, is investigated to show the imperfection with different scaling factors.
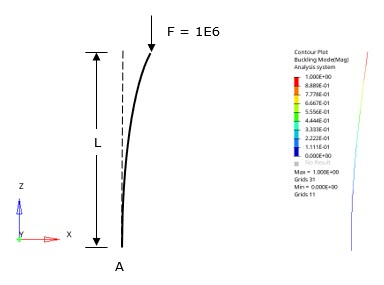
Figure 2. Model Details and First Buckling Mode of the Structure
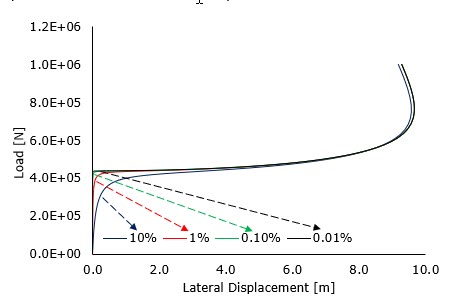
Figure 3. Load versus Lateral Displacement Plots. for different values of imperfection
Example 2: Post-buckling of a Cylindrical Roof with a Single Point Force
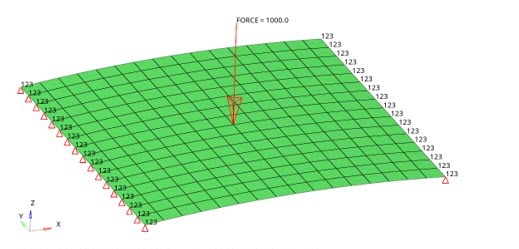
Figure 4. Model with Boundary Conditions
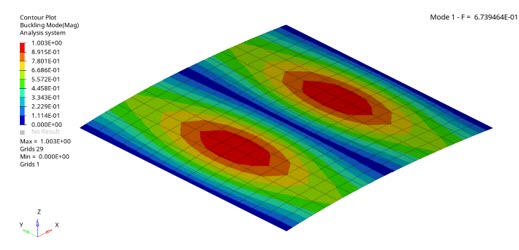
Figure 5. 1st Buckling Mode
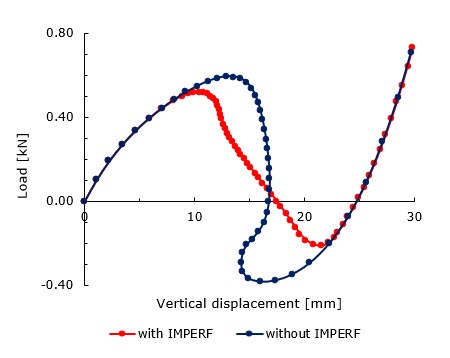
Figure 6. Load-Displacement Curve of the Cylindrical Roof from OptiStruct
Comments
- Imperfection is supported for nonlinear static and nonlinear direct transient for both small and large displacement analyses.
- In the presence of imperfection, element checking is still based on the perfect mesh.
- The magnitude of imperfection is not checked internally. It remains your responsibility to specify an imperfection that is physically correct.
- Initial stress condition can be specified independently of the imperfection.
- Multiple imperfections can be specified for different subcases in the same input file.
- In the case of subcase continuation (CNTNLSUB), imperfection can only be specified in the first subcase. In other cases, it would lead to an error.
- The output of displacement in the results files (for example, H3D) does not contain the value of imperfection. The output of displacement and strain is based on the imperfect configuration.
- The imperfection shape and scaling factors depend on the structural boundary conditions and the type of loading. The suitable combination of buckling modes and their scaling factor must be chosen according to your requirement, which could be from experimental reference. The imperfection must be large enough to capture the buckling behavior but must also be suitably small enough to guarantee the accuracy of the results.