Cyclic Symmetry Analysis
Cyclic symmetry is a type of symmetry in which a representative (or basic) segment, if patterned circularly about an axis of symmetry would result in the full model.
Structures with symmetry can often be modeled with one representative entity, from which the full structure can be obtained after certain operations (pattern, mirror, rotation, etc.). Such methods can lead to huge savings in modeling effort, computational time, and file storage. Therefore, exploiting symmetry in finite element models could prove to be very advantageous.
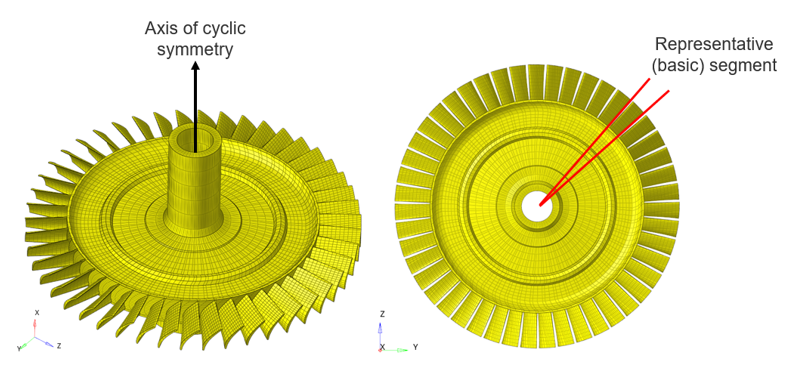
Figure 1. Cyclic symmetry in a gas turbine compressor wheel
- The basic segment could either be the smallest repeating unit in the model or could involve several repeating units.
- Depending on the user’s requirements, a full 360 degree model or a partial (as in, 270 degrees) model could be analyzed by suitably specifying the number of segments in the model definition.
In OptiStruct
In a cyclic symmetry analysis, the boundaries on either side of the modeled base segment which are to be connected to adjacent segments are defined as SIDE 1 and 2. The direction of the axis of symmetry are determined using the right-hand thumb rule.
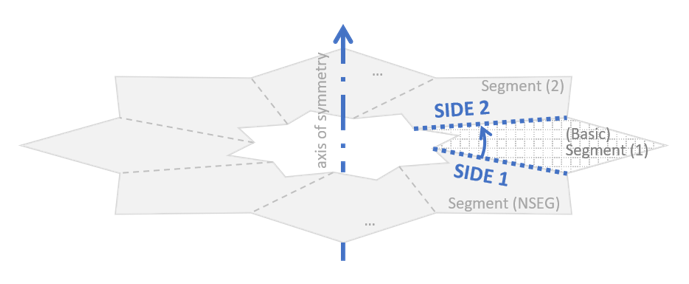
Figure 2. Axis of symmetry and sides of the basic segment
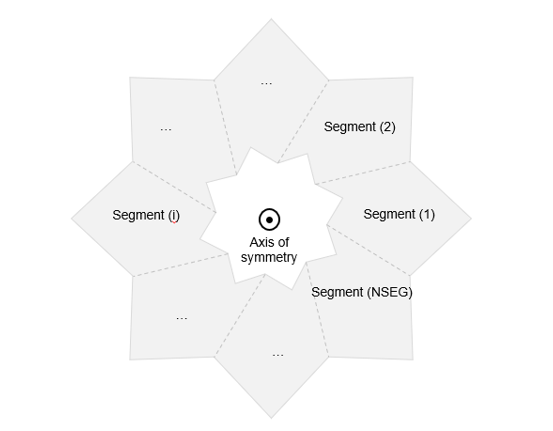
Figure 3. Numbering of the segments when the axis of symmetry is perpendicular to and out of the plane
In a cyclic symmetry analysis, the response of the full model is determined from a linear combination of several independent basic responses, known as solution harmonics. They are represented using indices called harmonic indices and they could be selected by the user during the modeling process.
The harmonic indices are supposed to be non-negative and must be no greater than (NSEG is the number of segments to be modeled).
| Analysis Type | Comments |
|---|---|
| Linear Static Analysis with Cyclic-symmetric loading |
|
| Linear Static Analysis with Non-cyclic-symmetric loading | In this case, only the 0th Harmonic will be used, and all other harmonics will be disregarded. |
| Normal Modes Analysis | Removing some harmonics will only lead to some missing mode shapes, without any loss in accuracy. |
| Entry | Purpose | Additional Details |
|---|---|---|
| HARMONICS | Specifies the solution harmonics to be used. |
|
| NOUTPUT | Specifies the segments for which results must be recovered and output. |
|
| Entry | Purpose | Additional Details |
|---|---|---|
| CYAX | Specifies the grids that lie on the axis of symmetry. | This entry is optional for cyclic symmetry analysis. |
| CYJOIN | Specifies grid points on the segment boundaries that connect to adjacent segments. |
|
| CYSYM | Specifies the number of segments in the model. | This entry is mandatory for cyclic symmetry analysis. |
| LOADCYH | Specifies the harmonic coefficients of loading. |
|
| LOADCYN | Defines the loading. |
|
Support Information
| Category | Supported Entities | Additional Details |
|---|---|---|
| Analysis type | Linear static analysis Normal modes analysis |
In normal modes analysis, only Lanczos eigensolver (EIGRL) is supported. |
| Analysis output | DISPLACEMENT STRESS STRAIN |
|
| Elements | CBEAM CTRIA3, CTRIA6 CQUAD4, CQUAD8 CTETRA, CHEXA, CPENTA |
|
| Constraints | MPC RBE2 RBE3 |
RBE2 and RBE3 will be generated only for the base segment in the result plot. |
| Materials | MAT1 MAT2 MAT9 MATT1 MATT2 MATT9 |
|
| Loads | Enforced displacement (only via non-zero
SPC) Forces Pressures GRAV RFORCE TEMP |
|
| Preloading | Preloaded linear static and normal modes analysis are supported | The following restrictions apply to the subcase that
preloads:
|
Problem Setup
$ *************************************************************
$ EXAMPLE TO DEMONSTRATE A CYCLIC SYMMETRIC ANALYSIS SETUP
$ *************************************************************
.
.
NOUTPUT = ALL
SUBCASE 101
SPC = 1
LOAD = 14
SUBCASE 102
SPC = 1
METHOD(STRUCTURE) = 2
HARMONICS = 102
BEGIN BULK
$--1---><---2--><---3--><---4--><--5---><--6---><---7--><--8---><---9-->
CORD2C 11 0 0.0 0.0 0.0 0.0 0.0 1.0
+ 1.0 0.0 0.0
EIGRL 2 0.0 50 MAX
SET 102 MODE
+ 0 1
CYSYM 4
CYAX 100
CYJOIN 1 12 THRU 20
CYJOIN 2 22 THRU 30
FORCE 51 12 11 1.0 0.0 100.0 1.0
LOADCYN 14 0.1 1.0 51
.
.Example
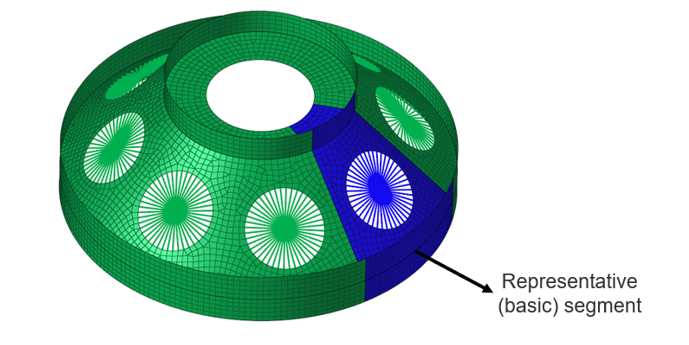
Figure 4. Cyclic symmetry model

Figure 5. Boundary conditions in the model. SPC's shown in red; pressure load is shown in green

Figure 6. Grid points in CYJOIN entry on each side of the model

Figure 7. Comparison of displacements between full model and cyclic symmetric model
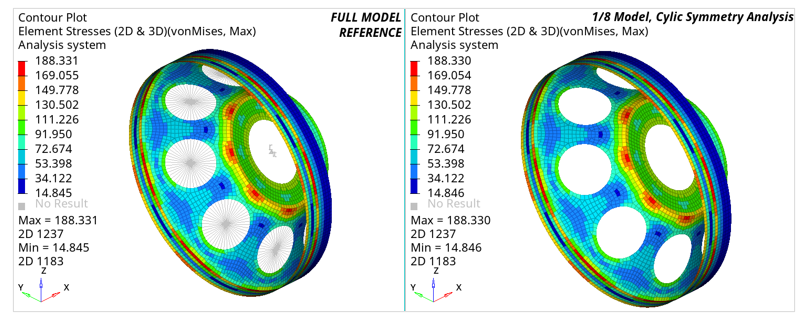
Figure 8. Comparison of element stresses between full model and cyclic symmetric model
Comments
- HyperMesh support for cyclic symmetry analysis would be available in future releases.