Phase 2: Shell Flat Plate
The objective is to create linear static models for shell models.
Launch HyperMesh and Set the OptiStruct User Profile
Import the Model
Set Up the Model
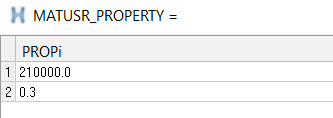
Create Material Properties
Create the material and property collectors before creating the component collectors.
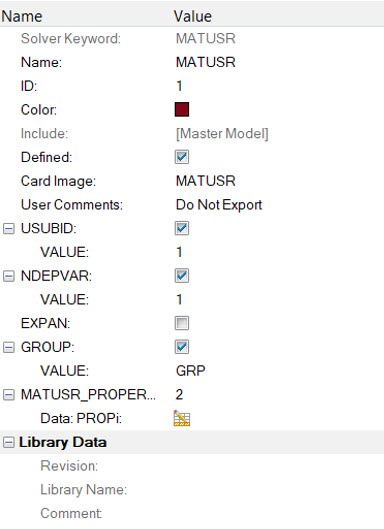
Define User Material
smatusr subroutine to accept the
two material properties (E and NU) and assemble the constitutive material model
matrix for use in the analysis. For more information, refer to User-Defined Structural Material in the User Guide.- While writing Fortran code you must follow the guidelines and syntax properly.
SMATUSRsubroutine is only used when the problem is linear or SMDISP.
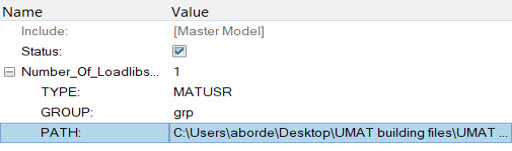
Build External Libraries
- Save the .dll or .so file in the same repository so that it can be accessed easily when required.
- The path of the dynamic library should be the same as mentioned in the LOADLIB card.
- Verify that the library path, name, and extension are correct before solving the problem. Also, check that the library was compiled and linked properly with the problem.
umat.F file using the
GNU Fortran Complier on Linux.
# rename the Fortran file for convenience
mv umat_barebones.F umat.F # optional
# compile and create object files
f95 -fPIC -c umat.F -o umat.o
# create the final shared library
ld -shared umat.o -o umat.so
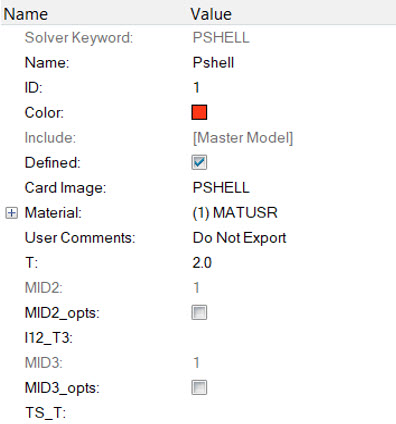
# The shared library “umat.so” can now be used via LOADLIB entry in the OptiStruct runCreate PSHELL Property
Link Material and Property to Existing Structure
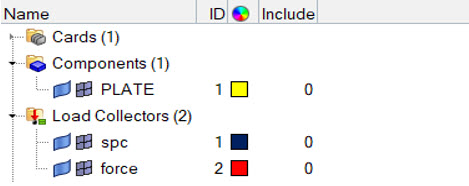
After the material and property are defined, they will need to be linked to the structure.
Create SPC Load Collector
Two load collectors will be created in this step.
Create Constraints
Here you will create constraints at one end of cylinder.
Apply Force
This step shows how to apply force on the other end of the cylinder.
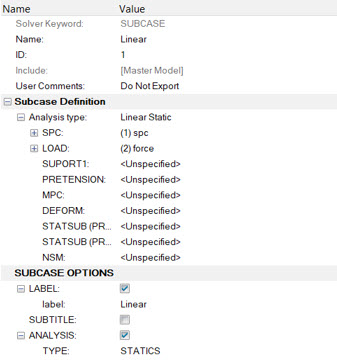
Create Linear Load Step
Here you will create an OptiStruct subcase (also referred to as a loadstep).
Select the Shared Library
Submit the Job
- Flat_plate.html
- HTML report of the analysis, providing a summary of the problem formulation and the analysis results.
- Flat_plate.out
- OptiStruct output file containing specific information on the file setup, the setup of your optimization problem, estimates for the amount of RAM and disk space required for the run, information for each of the optimization iterations, and compute time information. Review this file for warnings and errors.
- Flat_plate.h3d
- HyperView binary results file.
- Flat_plate.res
- HyperMesh binary results file.
- Flat_plate.stat
- Summary, providing CPU information for each step during analysis process.
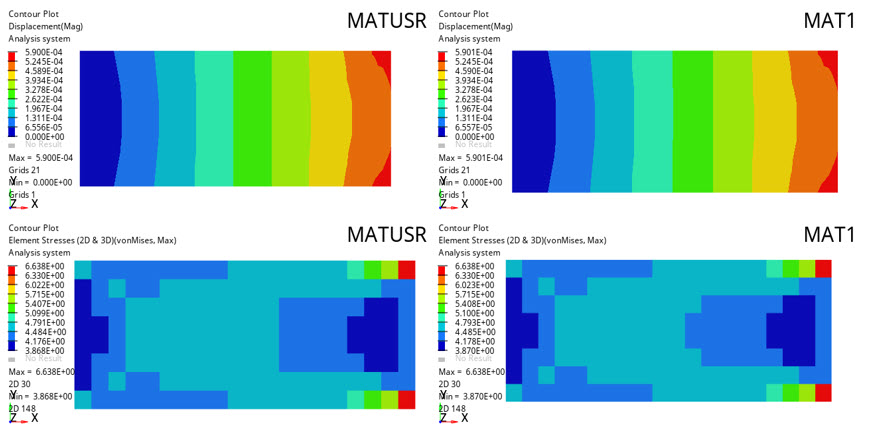
View the Results
Displacement and Stress results are output from OptiStruct for linear static analyses by default. The following steps describe how to view those results in HyperView.
 .
. 


 .
.  .
.