Theory and Equations

The engine and the clutch are modeled as mathematical equations in the IC Engine Powertrain. The state of the Engine is determined by engine speed and the Clutch by the Clutch slip. Following is a list of symbols used to describe the model in this section:

Engine Speed [State]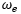
Clutch Slip [State]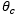
Clutch Torque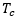
Engine Torque
Clutch Clamp Force Factor
Engine Inertia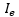
Clutch Stiffness
Clutch Damping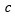
Transmission RPM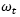
Clutch Capacity

Engine model

The engine is modeled as a black-box that produces a torque based on the current throttle position (input) and engine speed (state). The rotational inertia of all the rotating components of the engine are lumped in 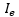. The torque to accelerate the engine’s rotating components is the difference between the torque the engine produces and torque reacted by the clutch. Hence, the derivative of the engine state (speed) is given by:

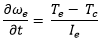
The engine torque is:

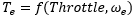
which is interpolated from a 3-D spline that is an input in the .pwr file.

Clutch model

The clutch is modeled as a stiff spring and damper that has the capability of transmitting torque from the engine to the gear box based on the clutch demand input signal. The output clutch torque (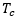) is an input to the gearbox.

The state of the clutch is defined by the clutch slip (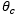). The clutch torque is determined by the equation:

This clutch torque is further saturated between -

and +

to ensure the clutch capacity is not exceeded. CFF is the Clamp Force Factor, it is determined by running the clutch demand through a step function as shown in the diagram below (which assumes clutch scaling = 1.0):

The clutch demand is the driver’s input on the clutch pedal. Clutch demand is non-dimensional: zero (0) clutch demand represents the driver’s foot off the clutch-pedal, while one (1) clutch demand represents the driver pushing the clutch-pedal to the floor. The derivative of the clutch slip state is determined by the following equation:

Where the AWC is the anti-windup component described below.

Anti-windup system

When the clutch is disengaged and subsequently re-engaged, some residual clutch slip is induced into the clutch that keeps the clutch slip at a non-zero value while disengaged. However, in a real situation the plate is free during the disengaged period and the clutch slip must return to zero in a finite time (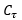) after the disengagement. This has to be modeled into the system. Hence, the AWC component is included into the derivative of the clutch slip which would cause the clutch slip to go to zero.

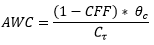
Anti-Stall system

The anti-stall system is an optional system that can be switched on and off in the powertrain depending upon the anti-stall flag model parameter. If the vehicle is put into neutral, or the clutch is disengaged for a long period of time, then the engine must return to its idling speed. This however does not occur many times since torque maps have negative torque corresponding to no throttle condition. To avoid the engine stalling, the model has the capability to modulate the throttle signal at low engine speeds (lower 20% of the rev band) such that sufficient throttle is applied for when the engine torque is set to zero at the idling speed.

Note: The anti-stall system is only in place to prevent an idling engine from stalling, the engine might still stall if the vehicle is in gear and the clutch is engaged.

Rev-limiter

The rev-limiter is an optional system that can be switched on and off in the powertrain depending upon the rev-limiter flag model parameter. This prevents the engine speed from exceeding the engine rev-limit by cutting throttle when the engine speed exceeds the limit.