Layered Dielectric Sphere
With this option a layered dielectric sphere located at the origin is taken into account with the Green’s function.
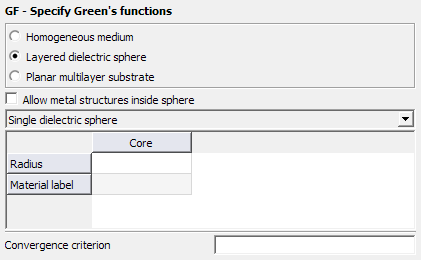
Figure 1. The GF - Specify Green's functions dialog, set to Layered dielectric sphere.
Parameters:
- Configuration list
- The drop-down list allows selecting between a Single
dielectric sphere, a Core and a coating layer and a
Core and three layers.Note: If metal structures are included, the only options are Single dielectric sphere and Core and two layers.
- Allow metal structures inside sphere
- When this item is checked metallic structures can be present in the inner parts of the sphere.
- Convergence criterion
- Convergence criteria for the summation of the rows of Green’s functions. If this field is 0 or undefined, a sensible standard criterion is used.
- Radius
- Radius of the sphere / layer in metres (is scaled by the SF card). For the layers, this is the total radius of the core plus layers up to that point. The highest numbered layer is on the outside of the sphere.
- Material label
- Label of the material (as defined in the DI card) to be used for the core / layer.

Figure 2. Example of a sphere consisting of 4 media (core and 3 layers) indicating the layer numbering.