応力-寿命(S-N)アプローチ
S-N曲線
S-N曲線は、最初にWöhlerによって開発され、応力と破壊のサイクル数との関係が定義されます。

Figure 1. 実験からのS-Nデータ

Figure 2. 両対数スケールでの1セグメントS-N曲線
セグメント1に対して
ここで、公称応力のレンジ、は破壊する疲労サイクル、は最初の強度指数、は疲労強度指数です。
S-N アプローチは弾性的な繰り返し荷重に基づき、S-N 曲線は寿命軸上の、1000 サイクル以上の数の範囲にあるはずとの推定に基づいています。このことは大きな塑性は起こらない、ということを保証します。これは一般に高サイクル疲労と言われます。
S-N曲線データは、Materialsモジュールを使用して指定された材料に関して提供されます。
複数SN曲線
- 複数平均S-N曲線: さまざまな平均応力で定義されたS-N曲線のグループ。
- 複数比S-N曲線: さまざまな応力比Rで定義されたS-N曲線のグループ。
- 複数Haigh図: さまざまなサイクル数で定義されたHaigh曲線のグループ。
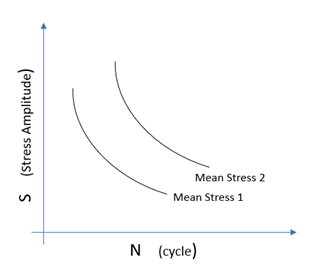
Figure 3. 複数平均S-N曲線
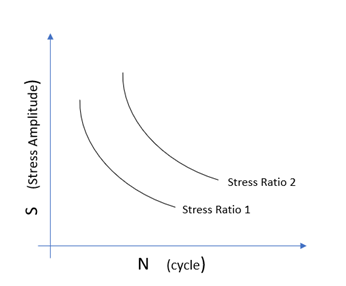
Figure 4. 複数比S-N曲線
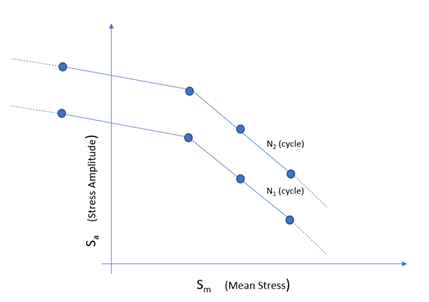
Figure 5. 複数Haigh図
レインフローサイクルカウント
サイクルカウントはランダム荷重履歴から離散的で単純な "等価"な一定振幅サイクルを取り出すために用いられます。
"サイクルカウント"を理解する1つの方法は応力-ひずみ関係を、時刻との対比に変更したものとして捉えることです。サイクルカウントは応力-ひずみ関係のヒステリシスループの数をカウントし、その範囲/平均値または最大値および最小値の記録をつけます。
- 単純な荷重履歴:
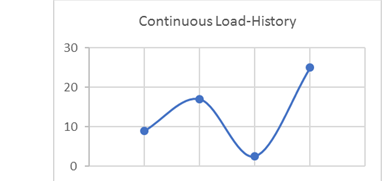
Figure 6. 連続した荷重履歴この荷重履歴は連続的であるため、山と谷のみから成る荷重履歴に変換されます。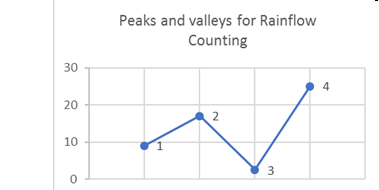
Figure 7. レインフローカウントについての山と谷. 1、2、3および4は4つの山と谷です。荷重履歴においてポイント4は応力の山(最大)であることが明らかであり、再配列中に前面に移動されます(Figure 8)。再配列後、山と谷は便宜のため再番号付けされます。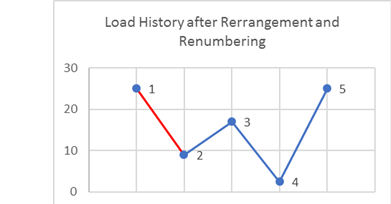
Figure 8. 再配列および再番号付け後の荷重履歴次に、最初の3つの応力値(1、2および3)をピックし、サイクルが存在するかを見極めます。
が応力値、ポイントを表すとすると:(2) (3) であるため、ポイント2から3までのサイクルが抽出されます。これで1つのサイクルが抽出され、2つのポイントがグラフから消去されます。
Figure 9. 残りのポイントの消去と再結合残りのポイントについて、同じプロセスが適用されます:(6) (7) この場合、であるため、ポイント1から4までの別のサイクルが抽出されます。これら2つのポイントも破棄された後は、ポイント5だけが残ります; したがって、レインフローカウントプロセスは完了となります。
2つのサイクル(2→3および1→4)が、この荷重履歴から抽出されました。最も高い山 / 谷を選択し、荷重履歴を再配列する主な理由の1つは、最も大きなサイクルが常に抽出される(この場合は1→4)ことを確実にすることにあります。再配列の前に荷重履歴を見て同じレインフローカウントプロセスを実行すると、1→4のサイクルが抽出されないことは明らかです。
- 複雑な荷重履歴レインフローカウントプロセスは、荷重履歴のポイント数にかかわらず同じです。ただし、再配列に使用される最も高い山 / 谷の位置によっては、再配列プロセスがどのように行われるかがはっきりしない場合もあります。Figure 10は、より複雑な荷重履歴の再配列プロセスだけを示しています。後続のレインフローカウントは、上記の単純な例で挙げているプロセスの外挿に過ぎず、ここでは繰り返しません。
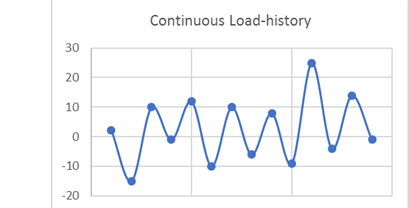
Figure 10. 連続した荷重履歴この荷重履歴は連続的であるため、山と谷のみから成る荷重履歴に変換されます。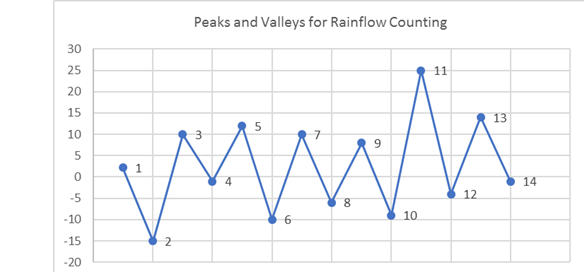
Figure 11. レインフローカウントについての山と谷明らかに、荷重ポイント11は荷重の最大値であり、したがって、荷重履歴はここで再配列、再番号付けされます。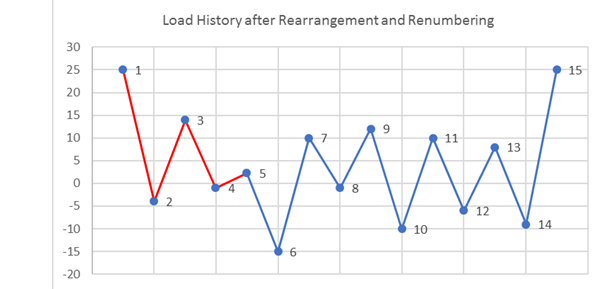
Figure 12. 再配列および再番号付け後の荷重履歴荷重履歴は、最大荷重後も含めすべてのポイントが荷重履歴の最初に移動され、荷重履歴の最後から消去されるよう再配置されます。
等価相当応力
S-N 理論は単軸応力を扱うため、それぞれの計算点、それぞれの時間ステップにおける応力成分は1つの統合された値にする必要があり、そこで、等価な公称応力が用いられ、S-N 曲線に適用されます。
さまざまな応力の組み合わせタイプが利用可能で、デフォルトは “Absolute maximum principal stress (絶対値最大の主応力)”です。脆性材料には "Absolute maximum principal stress"が推奨されますが、延性材料には"Signed von Mises stress"が推奨されます。符号付きパラメータの符号には最大絶対値主値の符号が用いられます。
"臨界平面応力 "は、単軸計算用の応力組合せ(応力寿命とひずみ寿命)としても利用できます。
例えば、要求された飛行機の数が20機の場合、10度ごとに応力が計算されます。
デフォルトではHyperLifeは、要求された平面の数に加え、𝜃 = 45および135度の面もでも計算します。これは、これらの飛行機で発生した場合の最悪の被害も含めてのことです。
平均応力補正
一般的に S-N 曲線は完全反転の繰り返し荷重の標準の試験から得られます。しかし、本来の疲労荷重は、完全なものではなく、平均応力は部品の疲労性能上で大きな影響を与えます。疲労強度に関して引張りの軸平均応力は有害ですが、圧縮の軸平均応力は有益です。平均応力修正は0でない平均応力の影響を考慮するために用いられます。
Haigh'座標のGerber放物線とGoodman線が平均応力の影響を考慮する際に広く用いられており、これらは次のように表すことができます:
Gerber
Goodman
SN曲線が応力比R=-1の曲線の場合
Gerber2
負の平均応力の影響を無視することによりGerber法を改善します。
SN曲線が応力比R!=-1の曲線の場合
の場合、Gerberと同じ
の場合、
Soderberg
GOODMANと僅かに異なり、平均応力は、極限引っ張り応力ではなく降伏応力により正規化されます。
- 等価応力振幅
- 応力振幅
- 平均応力
- 降伏応力
FKM

Figure 14.
HyperLifeでは、FKM補正に2つのオプションが使用できます。これらは、FKM MSSを、Assign Materialダイアログの1 slope4 slopesに設定することで有効になります。
- Regime 1 (R > 1.0)
- Regime 2 (-∞ ≤ R ≤ 0.0)
- Regime 3 (0.0 < R < 0.5)
- Regime 4 (R ≥ 0.5)
- 平均応力補正後の応力振幅(耐久応力)
- 平均応力
- 応力振幅
- 領域2について入力された勾配
平均応力補正に対して4つすべての勾配が指定された場合は、対応する平均応力感度値が4つすべての領域を制御する勾配になります。FKM-Guidelinesに基づき、Haigh図は応力比()の値をベースに4つのレジームに分割されます。続いて、補正値を使って損傷および寿命計算ステージのためにS-Nカーブが選択されます。
- Regime 1 (R > 1.0)
- Regime 2 (-∞ ≤ R ≤ 0.0)
- Regime 3 (0.0 < R < 0.5)
- Regime 4 (R ≥ 0.5)
- 完全反転の疲労強度(耐久応力)
- 平均応力
- 応力振幅
- 各領域における勾配
Interpolate
- 複数平均SN曲線
- 寿命は、通常、平均応力に関する2つのSN曲線の補間によって決定されます。以下に示す対数関数は常用対数関数であることに注意してください。
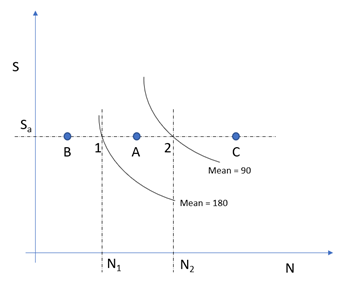
Figure 15. - ケースA
- サイクルに点Aにおける150MPaの平均応力が含まれている場合は、HyperLifeがFigure 15で点1と点2を探します。その後で、HyperLifeが平均応力に関するlogN1とlogN2を線形補間し、平均応力150MPaにおけるlogN_Aを決定します。logN_Aが決定されたら、寿命(N_A)と対応する損傷を決定できます。
- ケースB
- サイクルに曲線セットの最大平均応力(このケースでは180MPa)を上回る平均応力が含まれている場合は、HyperLifeがその動作を選択するための2つのオプションを提示します。
- オプション1、Curve Extrapolation = False
- 最大平均応力のSN曲線(このケースでは平均応力180MPaのSN曲線)を使用します。HyperLife内の例では、N1がHyperLifeから報告される寿命です。
- オプション2、Curve Extrapolation = True
- 2つのSN曲線のlog(N)を最大平均応力値で外挿します。Figure 15内の例では、log(N)が平均応力に関するlog(N1)とlog(N2)から外挿されます。
- ケースC
- サイクルに曲線セットの最小平均応力(このケースでは90MPa)を下回る平均応力が含まれている場合は、HyperLifeが最小平均応力のSN曲線を使用して寿命を決定します。Figure 15内の例では、寿命がN2になります。
- 複数応力比SN曲線
- 寿命は、通常、平均応力に関する2つのSN曲線の補間によって決定されます。複数応力比SN曲線が使用されている場合、HyperLifeは、応力比が1以上のSN曲線が定義されないと仮定します。このSN曲線は、圧縮応力または0応力振幅のSN曲線になります。以下に示す対数関数は常用対数関数です。Rは応力比を表します。
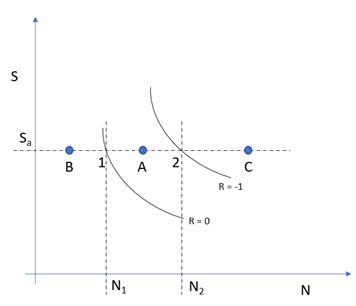
Figure 16. - ケースA
- サイクルに点AにおけるR=-0.2が含まれている場合は、HyperLifeがFigure 16で点1と点2を探します。その後で、HyperLifeが平均応力に関するlogN1とlogN2を線形補間し、R=-0.2におけるlogN_Aを決定します。サイクルのR値と応力振幅が与えられれば、サイクルの平均応力を計算できます。logN_Aが決定されたら、寿命(N_A)と対応する損傷を決定できます。HyperLifeは補間に応力比を使用しないことに注意してください。これは、最大応力が0のときにRが無限大になるためです。
- ケースB
- サイクルに曲線セットの最大R(このケースではR=0)を上回るRが含まれている場合は、HyperLifeがその動作を選択するための2つのオプションを提示します。
- ケースC
- サイクルに曲線セットの最小R(このケースではR=-1)を下回るRが含まれている場合は、HyperLifeが最小RのSN曲線を使用して寿命を決定します。Figure 16内の例では、寿命がN2になります。
- 一定寿命Haigh図
- 寿命は、通常、応力振幅に関する2つのHaigh図の補間によって決定されます。以下に示す対数関数は常用対数関数です。
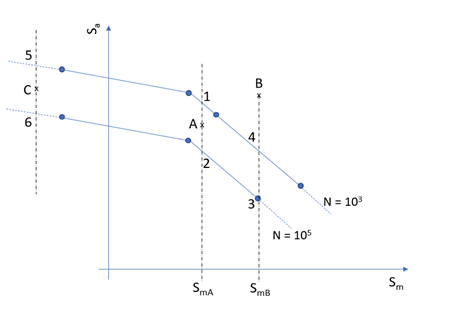
Figure 17.- 一定平均応力直線に対する補間
- Haigh図の線形補間に一定平均応力直線を選択した場合は、以下で説明するように、HyperLifeが一定平均応力直線に対して2つのHaigh図を補間します。
- ケースA
- サイクルに点Aにおける平均応力と応力振幅が含まれている場合は、HyperLifeがFigure 17で点1と点2を探します。点Aの寿命は1000~100000になるはずです。HyperLifeは、Sm_A一定平均応力直線に沿った応力振幅に関するlog(1000)とlog(100000)を線形補間し、点AにおけるlogN_Aを決定します。logN_Aが決定されたら、寿命(N_A)と対応する損傷を決定できます。
- ケースB
- 点(平均応力、応力振幅)がすべてのHaigh図の上または下に配置されている場合は、その点の寿命が2つの最大曲線または2つの最小曲線の外挿によって計算されます。Figure 17内の例では、log(1000)とlog(100000)がSm_B一定平均応力直線に沿った応力振幅に関して外挿されます。
- ケースC
- このケースでは、点5と点6における応力振幅が外挿から計算される可能性があります。2つの点で応力振幅が使用できるようになったら、ケースAで説明した手順が適用されます。
- 一定応力比直線に対する補間
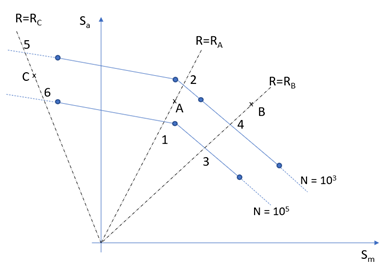
Figure 18.- ケースA
- サイクルに点Aにおける平均応力と応力振幅が含まれている場合は、HyperLifeがFigure 18で点1と点2を探します。点Aの寿命は1000~100000になるはずです。HyperLifeは、RA一定応力比直線に沿った応力振幅に関するlog(1000)とlog(100000)を線形補間し、点AにおけるlogN_Aを決定します。logN_Aが決定されたら、寿命(N_A)と対応する損傷を決定できます。
- ケースB
- 点(平均応力、応力振幅)がすべてのHaigh図の上または下に配置されている場合は、その点の寿命が2つの最大曲線または2つの最小曲線の外挿によって計算されます。Figure 18内の例では、log(1000)とlog(100000)がR=RB一定応力比直線に沿った応力振幅に関して外挿されます。
- ケースC
- このケースでは、点5と点6における応力振幅が外挿から計算される可能性があります。2つの点で応力振幅が使用できるようになったら、ケースAで説明した手順が一定応力比直線R=RCに適用されます。
複数平均SN曲線

Figure 19.
ケースA
サイクルに点Aにおける150MPaの平均応力が含まれている場合は、HyperLifeがFigure 19で点1と点2を探します。その後で、HyperLifeが平均応力に関するlogN1とlogN2を線形補間し、平均応力150MPaにおけるlogN_Aを決定します。logN_Aが決定されたら、寿命(N_A)と対応する損傷を決定できます。
ケースB
- オプション1、Curve Extrapolation = False
- 最大平均応力のSN曲線(このケースでは平均応力180MPaのSN曲線)を使用します。HyperLife内の例では、N1がHyperLifeから報告される寿命です。
- オプション2、Curve Extrapolation = True
- 2つのSN曲線のlog(N)を最大平均応力値で外挿します。Figure 19内の例では、log(N)が平均応力に関するlog(N1)とlog(N2)から外挿されます。
ケースC
サイクルに曲線セットの最小平均応力(このケースでは90MPa)を下回る平均応力が含まれている場合は、HyperLifeが最小平均応力のSN曲線を使用して寿命を決定します。Figure 19内の例では、寿命がN2になります。
複数応力比SN曲線

Figure 20.
ケースA
サイクルに点AにおけるR=-0.2が含まれている場合は、HyperLifeがFigure 20で点1と点2を探します。その後で、HyperLifeが平均応力に関するlogN1とlogN2を線形補間し、R=-0.2におけるlogN_Aを決定します。サイクルのR値と応力振幅が与えられれば、サイクルの平均応力を計算できます。logN_Aが決定されたら、寿命(N_A)と対応する損傷を決定できます。HyperLifeは補間に応力比を使用しないことに注意してください。これは、最大応力が0のときにRが無限大になるためです。
ケースB
ケースC
サイクルに曲線セットの最小R(このケースではR=-1)を下回るRが含まれている場合は、HyperLifeが最小RのSN曲線を使用して寿命を決定します。Figure 20内の例では、寿命がN2になります。
一定寿命Haigh図

Figure 21.
ケースA
サイクルに点Aにおける平均応力と応力振幅が含まれている場合は、HyperLifeがFigure 21で点1と点2を探します。点Aの寿命は1000~100000になるはずです。HyperLifeは、Sm_A一定平均応力直線に沿った応力振幅に関するlog(1000)とlog(100000)を線形補間し、点AにおけるlogN_Aを決定します。logN_Aが決定されたら、寿命(N_A)と対応する損傷を決定できます。
ケースB
点(平均応力、応力振幅)がすべてのHaigh図の上または下に配置されている場合は、その点の寿命が2つの最大曲線または2つの最小曲線の外挿によって計算されます。Figure 21内の例では、log(1000)とlog(100000)がSm_B一定平均応力直線に沿った応力振幅に関して外挿されます。
ケースC
このケースでは、点5と点6における応力振幅が外挿から計算される可能性があります。2つの点で応力振幅が使用できるようになったら、ケースAで説明した手順が適用されます。
損傷加算モデル
- ある応力の大きさの組み合わせと平均応力レベルにおけるS-N曲線からの材料の疲労寿命(破壊のサイクル数)。
- 荷重レベルにおける応力のサイクル数。
- 荷重サイクルにおける累積ダメージです。
線形損傷総和則は、周期疲労荷重による損傷の加算で荷重順序の効果を考慮しません。しかしながら、多くの応用でうまく機能することが実証されてきています。
安全係数
安全係数は、作用応力の履歴からの応力振幅に対する耐久限界または目標応力(目標寿命時)に基づいて算出されます。
- 平均応力 = 一定
- 応力比 = 一定
平均応力補正を適用した場合の安全係数(SF)は、次式で与えられます。
- 平均応力 = 一定
-
- GoodmanまたはSoderberg
SN曲線が応力比R=-1の曲線の場合
(20) = 修正されたSN曲線からの目標寿命に対する目標応力振幅
= 平均応力補正後の応力振幅
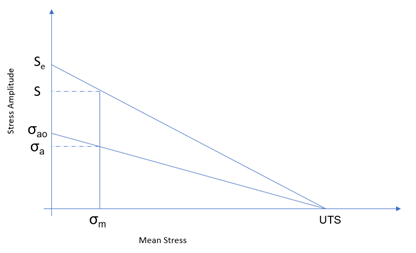
Figure 22.SN曲線が応力比R!=-1の曲線の場合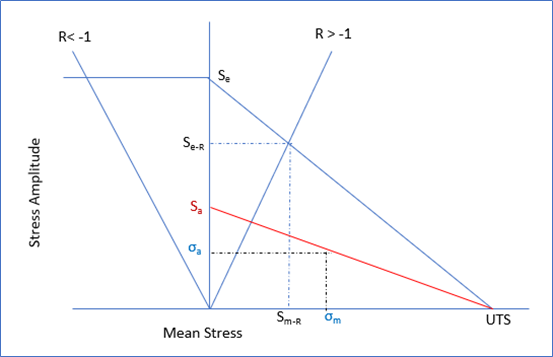
Figure 23.=応力振幅
=平均応力
=R比を持つSN曲線から取得された耐久限界
=に対応する平均応力
の場合、
(21) の場合、
の場合、
の場合、(22) - Gerber
(23) 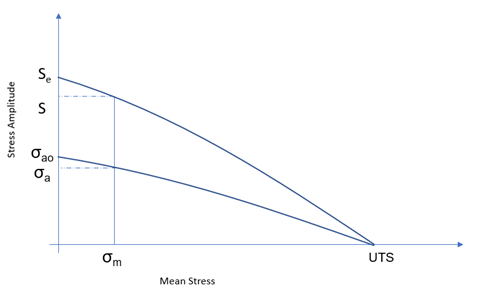
Figure 24.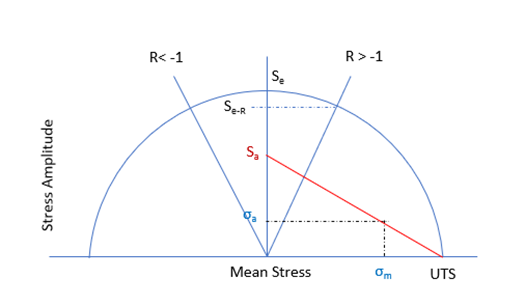
Figure 25.(24) (25) (26) (27) - Gerber2
-
(28) -
(29)
SN曲線が応力比R!=-1の曲線の場合
の場合、(30) (31) の場合、
の場合、
の場合、(32) -
- FKM
(33) -
(34) -
(35) -
(36) -
(37)
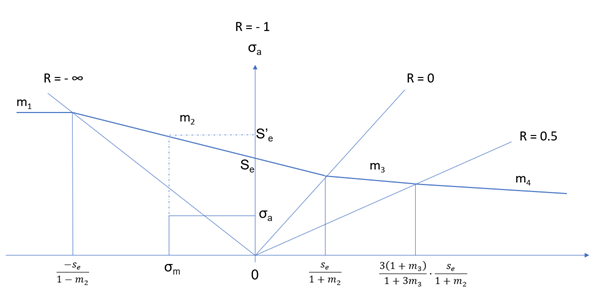
Figure 26. -
- 平均応力補正なし
(38)
- GoodmanまたはSoderberg
- 応力比 = 一定
-
- Goodman
SN曲線が応力比R=-1の曲線の場合
(39) 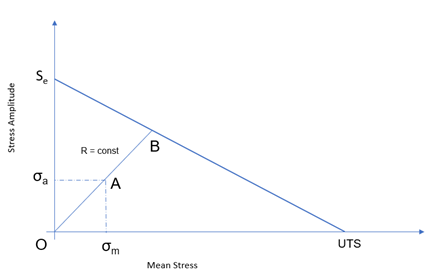
Figure 27.SN曲線が応力比R!=-1の曲線の場合
の場合、(40) の場合、
の場合、
の場合、
- Gerber
SN曲線が応力比R=-1の曲線の場合
-
(41) -
(42)
SN曲線が応力比R!=-1の曲線の場合(43) (44) の場合、
の場合、
-
- Gerber2
-
(45) -
(46)
SN曲線が応力比R!=-1の曲線の場合
の場合(47) (48) の場合、
の場合、
の場合、
-
- FKM
(49) = 定数R平均応力補正において修正された応力振幅
- 平均応力補正なし
(50) - Interpolate
- 複数平均を使用した安全係数
- 安全係数を計算するために、HyperLifeは、複数平均SN曲線を使用して、目標寿命で応力振幅と平均応力のペアを見つけることによって目標寿命の内部Haigh図を作成します。内部で作成されたHaigh図を使用して、HyperLifeは、「Haigh図」の章の「安全係数」の項で説明されているように、安全係数を計算します。Haigh図のデータ点の数は曲線の数です。そのため、曲線の数が多いほど、良い結果が得られます。Haigh図で平均応力範囲で利用できない場合は、HyperLifeがHaigh図を外挿します。
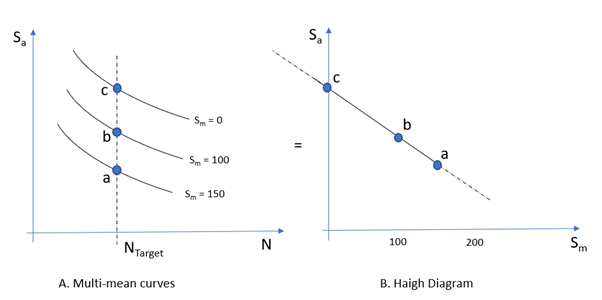
Figure 28. 複数平均曲線からHaigh図への変換 - 複数比を使用した安全係数
- 安全係数を計算するために、HyperLifeは、複数平均SN曲線を使用して、目標寿命で応力振幅と平均応力のペアを見つけることによって目標寿命の内部Haigh図を作成します。Haigh図のデータ点の数は曲線の数です。そのため、曲線の数が多いほど、良い結果が得られます。Haigh図で平均応力範囲で利用できない場合は、HyperLifeがHaigh図を外挿します。

Figure 29. 複数平均曲線からHaigh図への変換 - Haighを使用した安全係数
- 安全係数(SF)は、Figure 30で次のように計算されます。
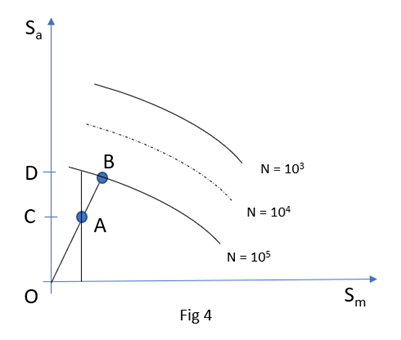
Figure 30.- 定数R: SF = OB/OA
- 定数平均: SF = OD/OC
- Goodman
複数平均を使用した安全係数

Figure 31. 複数平均曲線からHaigh図への変換
複数比を使用した安全係数

Figure 32. 複数平均曲線からHaigh図への変換