この方法の論理的側面

概要

本項では、エラー基準の計算が何に基づいているのかを説明する原理を紹介します。

この方法の原理

Fluxでは、補完的に解の誤差を決定できる2種類の方法を提供します。

1つ目の方法は、エネルギー保存、磁束密度の保存、熱流束の保存などの物理量の保存則に基づきます。

2つ目の計算方法は、随伴エネルギーの局所変化（勾配）の解析に基づきます。この方法は、物理的な意味があまりなく、エネルギー量が多ければ誤差も大きくなると仮定しています。

どちらの方法を選択しても、この計算は、各有限要素の式の局所評価となります。これにより、誤差が最も重要となる領域も可視化できます。各領域の誤差バランスを示し、さまざまな解析用に比較要素を提供します。

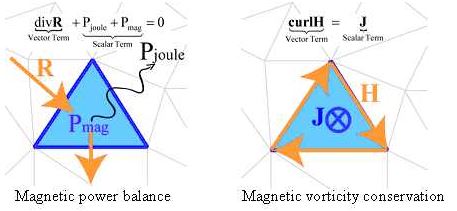
Fluxでの保存則

電磁気学では、多くの保存則を検証する必要があります。Fluxでは、以下の式が該当します：

• 電流の保存則：

div(J) = 0

ここでJは電流密度ベクトルです。

• 磁気誘導の保存則：

div(B) = 0

ここでBは磁気誘導ベクトルです。

• Maxwell-Gaussの方程式：

div(D) = ρ

ここでDは電気誘導密度ベクトル、ρは体積電荷密度です。

• 電力バランス方程式：

ここで、E×Hは電磁力密度ベクトル、J•Eは体積ジュール損失密度、 $H\bullet \frac{\partial B}{\partial t}$ は体積磁力密度です。

• 熱流束の保存：

div(J_t) = q

ここで、J_tは熱流束密度ベクトル、qは熱源の体積密度です。

随伴エネルギーの変化式

磁気随伴エネルギーおよび電気随伴エネルギーの勾配は、随伴エネルギーの変化（勾配）のスタディに基づいています。

• 磁気随伴エネルギーの勾配

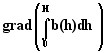
• 電気随伴エネルギーの勾配

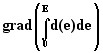
参考文献

詳細については、以下の論文をご参照ください：

Rondot L. , Mazauric V., Wendling P., « An Energy-Compliant Magnetodynamic Error Criterion for Eddy-Current Calculations », IEEE Trans.Magn., June 2010, Vol. 46 issue 6 p. 2353 - 2356