閉磁気回路: 磁気的接続性の問題(3D)
概要
ここでは、スカラーモデル(自動定式化)による3D問題での閉磁気回路の記述について説明します。
計算の原理に関する留意事項
Magneto Staticアプリケーションで方程式を解くために、次の2つのモデルが用意されています:
- ベクトルポテンシャルを使用するベクトルモデル
- スカラーポテンシャルを使用するスカラーモデル
スカラーモデル(自動定式化)では、有限要素法によって解く方程式はありません。問題の各領域には、固有の定式化が存在し、必然的に固有の方程式が存在します。したがって、領域間には境界が存在し、これにより定式化の結合が存在します。
接続性の問題
異なる電位間の結合は、そのような電位間の結合を許容する仮説がもはや有効ではないという意味で、禁止される場合があります。これは、接続性の問題を表します。
磁気的接続性の問題
磁気的接続性の問題は、透磁率の高い閉磁気回路の場合(トランスなど)に生じます。より正確には、複数のボリュームの磁気領域を貫く閉経路があり、この経路に沿ったHの線積分がゼロでない場合に生じます。
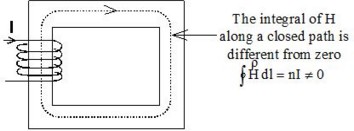
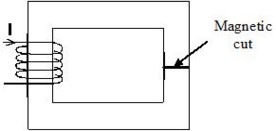
解決策: 切断面の概念
この問題を克服するには、磁気回路の切断面を作成する必要があります。これが、スカラーポテンシャルの飛躍を意味する“数学的切断面”です。切断面を貫く磁界のBとHの連続性は当然満たされています。
実際には、切断面は磁気的切断面エンティティを使用してモデル化されます:
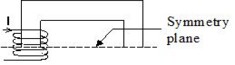
対称性と周期性
閉磁気回路が周期面または対称面で切断される場合は、切断面を追加する必要はありません。
例
- 接続性の問題を表す例
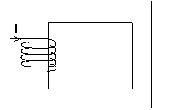
磁気回路が閉じられます。
- 接続性の問題がない例
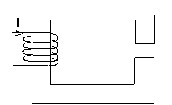
磁気回路に空隙が含まれるため
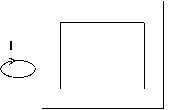
回路が閉磁気回路の“外部”にあるため