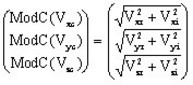絶対値関数：ModV、ModC、Mod

はじめに

絶対値関数（ベクトル絶対値、複素絶対値、一般絶対値）では、実数または複素数で表されるスカラー量とベクトル量の絶対値を計算できます。

絶対値関数について説明する前に、以下で表記について改めて説明します。

スカラー量： 表記

実数および複素数によって表されるスカラー量の絶対値関数を定義するには、以下の表記を使用します：

• 実スカラーの場合：A

• 複素スカラーの場合：I

  I = Ir + j Iiで表されます。

  ここで、IrとIiは実スカラーです。

ベクトル量： 表記

実数および複素数によって表されるベクトル量の絶対値関数を定義するには、以下の表記を使用します：

• 実ベクトルの場合：V

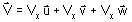  で表されます。

  ここで、Vx、Vy、Vzは実スカラーです。

• 複素ベクトルの場合：Vc

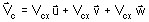  で表されます。

  ここで、Vcx、Vcy、Vczは複素スカラーです。

  複素ベクトルを次の形式で表すこともできます：

  $\overrightarrow{Vc}=\overrightarrow{Vr}+j \overrightarrow{Vi}=\left(\begin{array}{c}Vxr\\ Vyr\\ Vzr\end{array}\right)+j\left(\begin{array}{c}Vxi\\ Vyi\\ Vzi\end{array}\right)=\left(\begin{array}{c}Vxr+jVxi\\ Vyr+jVyi\\ Vzr+jVzi\end{array}\right)=\left(\begin{array}{c}Vcx\\ Vcy\\ Vcz\end{array}\right)$

  ここで、Vxr、Vyr、Vzr、Vxi、Vyi、Vziは実スカラーです。

ベクトル絶対値：ModV関数

ModV(X)関数は、Xベクトルのベクトル絶対値を返します。Xベクトルは、実ベクトルでもスカラーベクトルでもかまいません。

• Vが実ベクトルである場合、ModV(V)は、次の式によって表される実スカラーです：

• V cが複素ベクトルである場合、ModV(V c)は、次の式によって表される複素スカラーです：

  $ModV\left(Vc\right)=ModV\left(Vr\right)+j ModV\left(Vi\right)= \sqrt{Vxr²+Vyr²+Vzr²}+j \sqrt{Vxi²+Vyi²+Vzi²}$

複素絶対値：ModC関数

ModC(X)関数は、複素引数Xの複素絶対値を返します。複素引数Xは、複素スカラーでも複素ベクトルでもかまいません。

• Iが複素スカラーである場合、ModC(I)は、次の式によって表される実スカラーです：

• Vcが複素ベクトルである場合、ModC(Vc)は、次の式によって表される実ベクトルです：

一般絶対値：Mod関数

Mod(X)関数は、引数Xの一般絶対値を返します。引数Xのタイプ（スカラーまたはベクトル、実数または複素数）にかかわらず、Mod(X)の結果は実スカラーです。

• Iが複素スカラーである場合、Mod(I)は、次の式によって表される実スカラーです：

• V cが複素ベクトルである場合、Mod(V c )は、次の式によって表される実スカラーです：

概要

絶対値関数（ModV、ModC、Mod）の結果について、次の表で説明します。