定式化： 一般的な側面

概要

ここでは、状態変数、定式化、および定式化のモデルの概念を紹介します。

状態変数の概念

理論的な観点から見ると、それぞれの物理アプリケーションには1つの連立方程式が伴います。

この連立方程式を解くために、状態変数と呼ばれる計算の変数が使用されます。状態変数は、この連立方程式を1つまたは2つの方程式に簡略化します（その後、これらの変数からすべての電磁量を計算することができます）。

例：

• 電気アプリケーション： 状態変数は電位Vです。
• 熱アプリケーション： 状態変数は温度Tです。

定式化の概念

Flux内の領域ごとに、以下を示す1つの定式化が存在します：

• 何が状態変数なのか
• どのような方程式がどのように解かれるのか

例：

• 静電アプリケーション：（定式化ES3SCA）
  • 状態変数は電位V（Flux 3DではPHI1と表記されます）です。
  • 解かれる方程式：

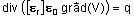
• 電気伝導アプリケーション：（定式化 EC3SCA）
  • 状態変数は電位V（Flux 3DではPHI1と表記されます）です。
  • 解かれる方程式：

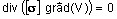
定式化とアプリケーション

電気アプリケーションと熱アプリケーションには、1つの解法のみが用意されています。このため、ドメインのすべての領域に対して、1つのFlux定式化しか存在しません（前の例をご参照ください）。

磁気アプリケーションには、さまざまな解法が用意されています。このため、ドメインの領域ごとに1つのFlux定式化を選択できます（下記をご参照ください）。

モデルの概念

磁気アプリケーションに用意されているさまざまな定式化は、まとめることができます。ここでは定式化のモデルについて説明します。

磁気アプリケーション内で用意されている2つのモデルは次のとおりです：

• 以下を使用するベクトルモデル： 磁気ベクトルポテンシャルAと電気スカラーポテンシャルV

• 以下を使用するスカラーモデル： さまざまな磁気スカラーポテンシャルϕと電気ベクトルポテンシャルT