概要 / 例

説明

状態変数（すなわち関連システムの未知数）が時間の関数である場合、問題は時間依存または過渡タイプと認識されます。以下に2つの例を示します。

例1（熱アプリケーション）

Thermal Transientアプリケーションで有限要素法を使用して解かれる微分方程式は次のとおりです：

ここで：

• [k]は熱伝導率のテンソル
• ρCpは体積熱容量
• qは熱源の出力の体積密度
• Tは温度（すなわち状態変数であり、システムの未知数です)

このケースでは、温度Tは時間の関数（1階微分方程式）です。

例2（磁気アプリケーション）

Transient Magneticアプリケーション（ベクトルモデルを使用）で有限要素法を使用して解かれる微分方程式は次のとおりです：

ここで：

• [ν]は計算ドメインでの磁気抵抗率のテンソル
• [σ]は計算ドメインの導電率のテンソル
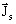• は電流源の密度
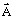• は磁気ベクトルポテンシャル（それぞれ状態変数、つまり、システムの未知数です）

この例では、磁気ベクトルポテンシャルAは時間の関数（微分方程式は1階）です。

時間離散化方程式

時間ドメインのステップバイステップと呼ばれる手法が、時間変数に関するこの最後の微分方程式の積分に適用されます。時間ドメインは、時間ステップと呼ばれる小さい時間間隔に分割されます。この時間間隔内では、未知数が時間に関して線形に変化すると想定されます。