1階微分システムの解析:オイラー法
1階微分システム: 記述
放物線タイプまたは双曲線タイプの偏導関数を使用した問題に対する有限要素法を適用すると、次の形式の1階微分システムを解くことになります:
![]() 。ここで、MとNは正則行列
。ここで、MとNは正則行列
代数変換を使用して、このシステムは次の形式で記述できます:
![]() (1)
(1)
![]()
時間離散化
すべての数値解法に共通の原則は、時間計算領域[t0, tmax]を短い間隔に離散化(時間ステップΔt ≡ hで特性が示される)するというものです。
X(t)の導関数は、時間的に連続する2つのXの値の差によって近似できます:
![]() (2)
(2)
接線法
接線法と呼ばれる最も単純な数値解法は、システム(1)内の導関数dX/dtを前述の近似(2)で置き換えるというものです。
これで、(1)方程式が次の形式で記述されます:
![]()
ここで、時間変数の値ti+1 = t0 + ihに対応する解は次のようになります:
![]()
この方法は、解曲線X(t)上の接線を使用して、ポイント(ti, Xi)からポイント(ti+1, Xi+1)を決定するため、接線法と呼ばれます。
接線法(続き)
そのシンプルさから使いやすい接線法ですが、数値解法での適切な精度を保証するには、非常に短い時間ステップhを選択する必要があります。精度に対する時間ステップサイズの影響を下の図に示します:
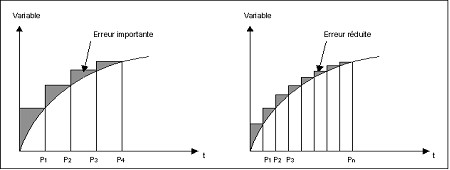
陽解法 / 陰解法
接線法より複雑だが、精度の高い方法が推奨されます。このような方法では、より長い時間ステップを選択できるため、計算時間が減少します。
本書では、これらの方法については詳しく説明しません。一部のデータ要素を下の2つの表に示します:
| 方法 ... | 説明 | |
|---|---|---|
|
“分離ステップ解法”または陽解法 |
時間ti+1におけるXの近似は、1つ前の時間tiにおける既知の変数を示唆するのみです。 |
導関数は、前の2つのステップによって計算されます:
|
|
“連結ステップ解法”または陰解法 |
時間ti+1におけるXの近似は、その時間におけるXの値を意味します。 |
導関数は、現在と1つ前のステップによって計算されます:
|
| 方法 | 利点 | 欠点 |
|---|---|---|
| 陽解法 | 実装が容易 | 多くの場合、数値的不安定の現象が生じるため、非常に短い時間ステップhを選択する必要がある |
| 陰解法 | より安定しており、より長い時間ステップを使用できる | 暗黙的な項により、時間ステップごとの計算量が増える |
半陰解法
この方法では、パラメータθとのその値(範囲が[0, 1])が導入され、時間ti+1に対応する解が次の式で与えられます:
![]()
ここで、![]()
最も使用されるスキームを定義するθの値を、次の表に示します:
| θの値 | 計算スキームの名前 |
|---|---|
| 1 | 陰 |
| 0.878 | リニガー |
| 2/3 | ガラーキン |
| 1/2 | クランク-ニコルソン |
| 0 | 陽 |
半陰解法は、θ ≥ 0.5の場合に無条件に安定します。最も使用される計算スキームは、θ = 1/2の場合に、優れた精度を示し、安定性が保証されるクランク-ニコルソンとして知られるスキームです。
Fluxでの作業
求める方程式は、時間変数に関する1階微分方程式です。この方程式は、陰解法によって積分されます。時間離散化間隔の最終値としてすべての量が計算されます。