2Dメッシュ

概要

次のような板状導体には2Dメッシュを使用します：

  • 導体の厚みが、その方向の電流密度の変化が無視できるほど十分に薄い
  • 電流経路の初期仮定が困難

この方法は、入出力電流端子の断面が小さく、スタディ対象とするデバイスの形状が平坦な、パワーエレクトロニクスに使用するバスバーに主に適用します。

原理

2Dメッシュでは、下図のように、平面導体全体を小さいサイズの基本プレートの集合に分割します。

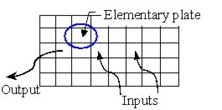
電流が流れる優先方向として平面導体の2つの主方向があるので、基本プレートはメッシュの2D要素です。

下図のように、電流密度が均一であると仮定した4つの部分電気回路を使用することによって、基本プレートをモデル化します。

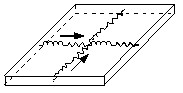
前に説明した解析の公式を使用すれば、4つの部分回路それぞれの部分抵抗（Ri）と部分インダクタンス（Li）、および複数の要素間の部分相互インダクタンス（Mij）を計算できます。

注: これらの値は周波数によって変化しません。

等価電気回路

基本プレートによる部分電気回路を関連付けることによって、板状ソリッド導体の等価電気回路が得られます。

2つのメッシュの境界で2つの抵抗と2つの相互連成インダクタが直列接続されている点に注意します。計算を簡素化するために、PEEC手法では、2つの抵抗と2つのインダクタの値が自動的に計算され、等価な1つの抵抗と1つのインダクタに置き換えられます。

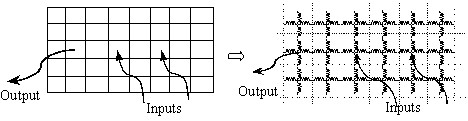
板状ソリッド導体等価電気回路の各種パラメータ値は周波数によって変化します。

注：

2Dメッシュのサイズが一定であると、ソリッド導体のプレートごとにメッシュを生成することで要素の数が膨大になることが考えられます。電流が流れる経路を想定することで、別のメッシュ化手法を適用することもできますが、妥当な電流経路の想定が困難なことがあります。