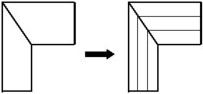
メッシュの概念
導体内の交流電流: 表皮効果 / 近接効果
部分インダクタンスを評価するためのPEEC法では、基本的に、導体断面において電流密度が均一であり、電流の優先経路が特定されていると想定されています。
しかし、次の理由から、これらの想定はソリッド導体の適用性を狭めます:
- 高周波では、電流密度は導体の表面に近いほど高くなる(表皮効果)
- 各導体はその周囲に影響を与え、電流線の分布変動、および抵抗、誘導、相互挙動の変動の一因となる(近接効果)
解決策: メッシュ
ソリッド導体内の表皮効果と近接効果を考慮するために選択された解決策は、導体を複数の基本導体に細分することです。これらの基本導体内では、電流密度は断面全体にわたって均一であると想定され、すでに定義されている式を適用できるようになります。
したがって、メッシュと呼ばれるこのステージは、ソリッド導体の場合に結果の精度を保証するために不可欠です。
以下では、メッシュを使用する場合の計算原理を簡単な例を通じて説明します。
原理(例)
長方形断面を持つ屈曲したチューブ状導体の等価インピーダンスの計算に注目します(特定の周波数で)。計算原理を次の表に示します。
| フェーズ0(初期フェーズ): 導体のメッシュ | |
|---|---|
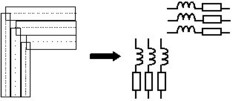
| 導体を複数の基本チューブ(1D要素)に分割
|
パラメータの(R、L)ペアを各1D要素に関連付け
|
| フェーズ1:PEEC計算(周波数に依存しない) |
|---|
|
各要素の抵抗と部分自己インダクタンス(R、L)の計算 すべての並列要素間の部分相互インダクタンス(M)の計算 |
| フェーズ2: 等価インピーダンスの計算(周波数に依存) |
|---|
| 要素の直列 / 並列接続による等価回路の構築
特定の周波数(f)におけるチューブ状導体の抵抗と等価インダクタンス(Re、Le)の計算 |
導体ごとに異なるメッシュ
導体の形状によってメッシュのタイプを使い分けることができます。
1Dと2Dのメッシュを次の表に示し、その後でこれらについて詳しく説明します。
3Dメッシュでは、電流の経路が不明なソリッド導体をモデル化できます(Flux PEECではまだ導入されていません)。
| メッシュ | 対象の導体 | 切断位置 | |
| 形状 | 説明 | ||
| 1D | チューブ状 |
電流の優先経路を特定できます(一方向電流)。 |
チューブ断面 |
| 2D | 板状 |
電流の優先経路を特定できません(双方向電流)。 |
電流が流れる平面 |