部分インダクタンスの概念

概要

インダクタンスの概念は、閉じたループのコンターにあてはめられます。インダクタンスの線積分の定義に基づいて、この合計インダクタンスは、多くのコンターセグメントの寄与を足し合わせたものと見なすことができます。1972年に、A. E. Ruehliは、PEEC法の基盤となっている部分インダクタンスの理論を提唱しました。この理論により、回路の各要素による、その回路の合計インダクタンスへの寄与を計算することができます。

この部分インダクタンスの概念を以下で説明します。

留意事項

コンターCによって定義され、電流Iが流れる閉ループ電流回路のインダクタンスは、この電流ループのコンターC上のベクトルポテンシャルAの線積分によって求められます。

この方程式は、次の条件下で有効です：

電流密度が一定である糸状ループ
電流の閉ループによって生じる磁界のドメイン内に非線形磁気材料が存在しない

原理

ここでは、C = S₁∪S₂∪S₃∪S₄が成り立つ電流の長方形ループの簡単な例について考えてみましょう。

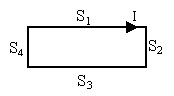
コンターC上のベクトルポテンシャルAの線積分は、長方形ループの4つの各セグメントに分割できます：

同様に、任意のポイントにおけるベクトルポテンシャルは、長方形ループの各セグメントの寄与の合計と見なすことができます：

したがって、このループのインダクタンスは、次の二重和によって表すことができます：

ここで、は、ループセグメントS_nによって生じるベクトルポテンシャルです。

部分インダクタンス：定義

上記で計算したループのインダクタンスは、次の二重和によって表すこともできます：

ここで、M_{P_mn}は、ループセグメントS_mとS_n間の部分インダクタンスを表します。

m ≠ nの場合、これは部分相互インダクタンスM_Pに該当します。

m = nの場合は、これは部分自己インダクタンスL_Pに該当します。

並列導体の平行六面体部分については、解析式を作成できます。これらの式は、解析式で示しています。

これらの部分（またはPEEC要素）が斜めに配置されている場合は、数値積分法を使用して部分相互インダクタンスを計算する必要があります。詳細については、準解析式をご参照ください。

これに対して、2つの垂直導体間の相互インダクタンスはゼロです。

一般化

この定式化は孤立したループのケースに限定されません。さらに複雑なシステムに拡張できます。

このようなシステムを複数の基本セグメントに分割することで、インダクタンスの正方対称マトリックスを得ることができます。このマトリックスで、対角項は部分自己インダクタンスに該当し、非対角項は部分相互インダクタンスに該当します。