OS-E: 0897 Multi-Material Topology Optimization of Automotive Chassis
Multi-Material Optimization (MMO) can be used in applications that require optimizing the parts of different materials. This method offers an initial concept-level look at material placement within the structure, where multiple materials can be evaluated.
The relationship between the mass savings, stiffness, and relative cost to manufacture the material can be included in the optimization formulation.
Without a consistent formulation, optimization would favor the lightest or stiffest material (steel or aluminum) but competing requirements can guide the design.
Multi-material optimization can be used when information outside of the structural performance is known that would influence total production costs, such as the relative price of different materials, and the relative volume production of each of them.
- Case 1:Objective: Topology optimization considering steel and aluminum individually
- Steel optimization
- Higher mass, less material to meet stiffness requirements.
- Aluminum
- Less mass, more material to meet stiffness requirements.
- Case 2:
Topology optimization considering multiple materials (steel + aluminum)
Objective: Minimize the total mass of steel and aluminum material in the structure.
Resulting design meets the stiffness requirement while removing material where unnecessary.
- Case 3:
Topology optimization considering multiple materials and minimizing relative cost.
Objective: Minimize cost function as a function of mass , where aluminum costs 50% more than steel.
Since the cost of aluminum is higher than steel, by taking this into account, look at where to place the material.
Model Files
Refer to Access the Model Files to download the required model file(s).
The model files used in this example include:
- case1_steel_optimization.fem
- case1_aluminum_optimization.fem
- case2_steel_aluminum_optimization.fem
- case3_steel_aluminum_optimization.fem
Model Description
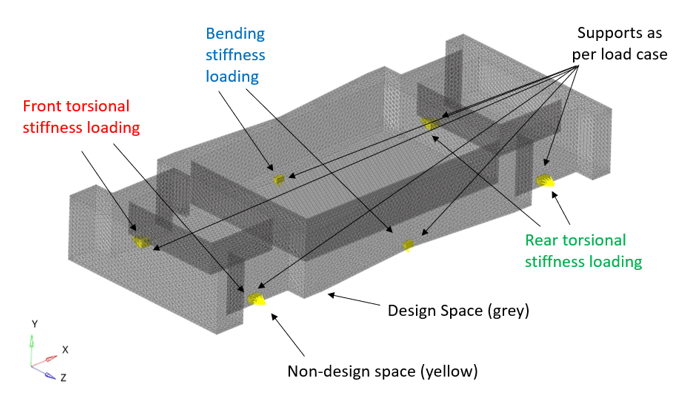
Figure 1. Chassis Model with Constraints and Loading Conditions
- Unit loads for three scenarios: bending, front torsional stiffness, and rear torsional stiffness
- Displacement constraints applied at all the loading locations based on baseline analysis
- Symmetry constraint at the mid-plane
- FE Model
- Chassis body
- CTETRA
- Connectors
- Rigid elements (RBE2)
- Aluminum
- Young's modulus
- 7E+04 MPa
- Poisson's ratio
- 0.33
- Density
- 2.7E-09 ton/mm3
- Steel
- Young's modulus
- 1.95E+05 MPa
- Poisson's ratio
- 0.29
- Density
- 9E-09 ton/mm3
Results
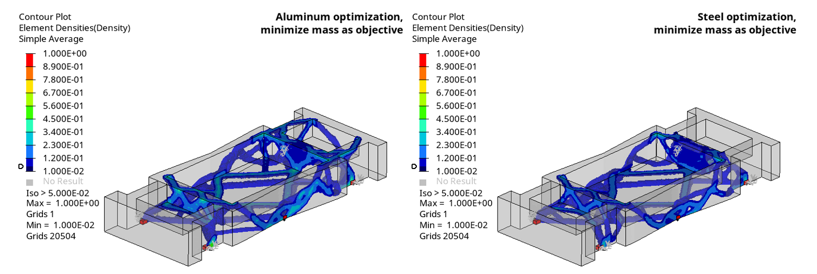
Figure 2. Case 1 Topology Optimization Results
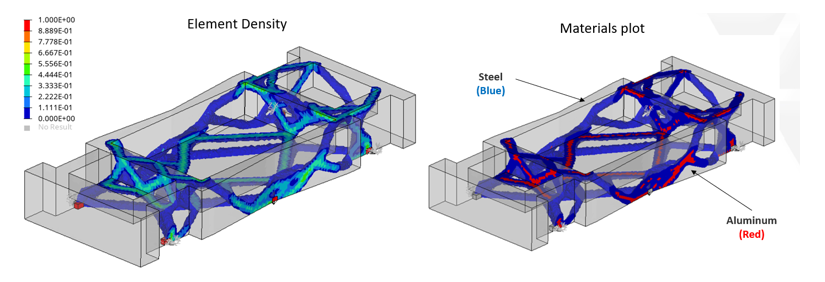
Figure 3. Case 2 Topology Optimization Results
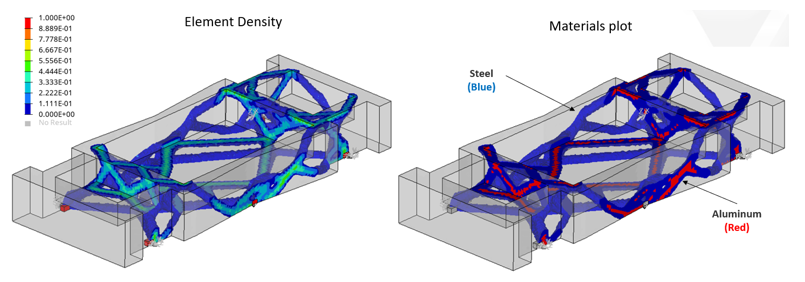
Figure 4. Case 3 Topology Optimization Results
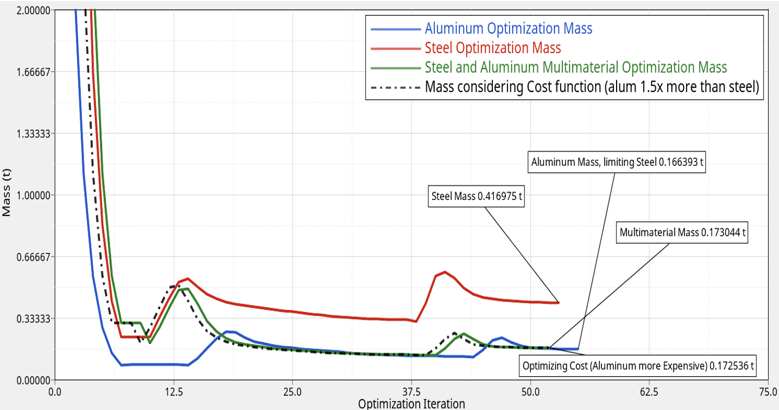
Figure 5. Results Comparison. tracking the mass over the optimization iterations for different scenarios